Edge-weighted graphs¶

In many applications, the edges in the graphs have some numeric weight/length/cost/etc associated to them. For instance, if a graph models a road map, then

the vertices are road crossings and endings,
the edges are roads connecting these, and
the edges are labeled with the length of road (i.e., the distance between the two points).

In a social network model, the edge weights could represent the number of messages exchanged between the connected people during the last month. In the abstract mathematical level, we call such numeric values on edges as weights. In the following, we extend the mathematical definitions for graphs (recall Section Mathematical definitions) to allow edge weights.

An edge-weighted undirected graph is a triple $$\Tuple{\Verts,\Edges,\UWeights},$$ where

$ \Verts $ is a (usually finite) set of vertices,
$ \Edges $ is a set of edges between the vertices, each edge being a pair of the form $ \Set{u,v} $ with $ u,v \in \Verts $ and $ u \neq v $, and
$ \UWeights: \Edges \to \Reals $ associates a real-valued weight to each edge.

Example

The graph shown below is $ \Tuple{\Verts,\Edges,\UWeights} $, where

the vertices are $ \Verts = \Set{a,b,c,d,e,f,g} $,
the edges are $ \Edges = \{\Set{a,b},\Set{a,e},\Set{a,f},\Set{b,c},\Set{b,d},\Set{b,f},\Set{c,d},\Set{c,e},\Set{d,g},\Set{e,f}\} $, and
the weights are $ \UWeight{a}{b} = 7 $, $ \UWeight{a}{e} = 6 $ and so on.

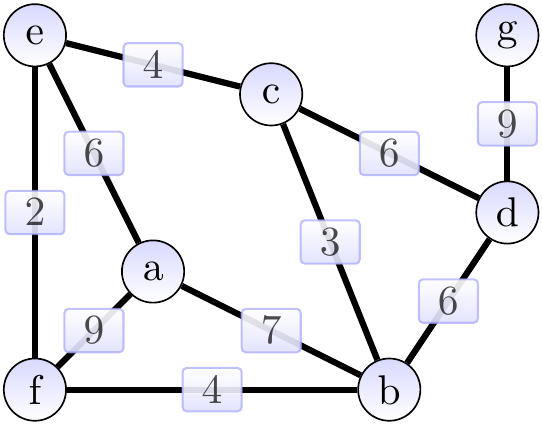
The edge-weighted directed graphs are defined similarly except that the edges are pairs of form $ \Tuple{u,v} \in \Verts \times \Verts $ as in the case of directed graphs without edge weights.

Paths, cycles, and trees are defined in the same way as for the graphs without edge weights.