Basics of Analysis of Algorithms

We want our algorithms to be efficient, in a broad sense of using the given resources efficiently. Typical resources and properties of interest include

running time,
memory consumption,
parallelizability,
disk/network usage,
efficient use of cache (cache-oblivious algorithms),
and so on.

Naturally, we may have to make trade-offs. For instance, an algorithm that uses less memory may use more time than another algorithm.

In this course, we mainly focus on running time. We study the running time of a program/algorithm as a function \(f(n)\) in the size \(n\) of the input or some some other interesting parameter. Both \(n\) and \(f(n)\) are assumed to be non-negative. This allows us to find out how the performance of the algorithm scales when the parameter \(n\) grows. To this end, we perform two kinds of analysis:

Apriori analysis that studies the algorithm description and tries to find out how fast the running time function \(f(n)\) grows when the parameter \(n\), such as the input size, grows. Here we are not interested in the exact values of \(f(n)\) but only the growth rate of \(f\). For instance, a linear-time algorithm is usually much better than a quadratic-time algorithm for the same computational task.
Experimental analysis, in which the exact running times of an implementation or many implementations are obtained, in a specific hardware and software setting, and then analyzed.

The big-O notation

As said above, in the apriori analysis we are usually interested in the asymptotic growth rate of functions. Thus we use the big-O notation and its variants. It is a mathematical tool that abstracts away small values of \(n\) and constant factors. In the context of running time analysis of algorithms,

small values of \(n\) correspond to small inputs, and
constant factor variations in the running time are caused by the clock speed and architecture of the processor, memory latency and bandwidth, applied compiler optimizations and so on.

Definition

For two functions, \(f\) and \(g\), we write \(f(n) = \Oh{g(n)}\) if there are constants \(c,n_0 > 0\) such that \(f(n) \le cg(n)\) for all \(n \ge n_0\).

That is, if \(f(n) = \Oh{g(n)}\), then \(f(n)\) is at most a constant factor larger than \(g(n)\) when we consider large enough values of \(n\). When \(f(n) = \Oh{g(n)}\), we thus say that grows at most as fast as \(g(n)\).

In addition to \(\BigOh\), “big-omega” and “big-theta” are also commonly used:

\(f(n) = \Omega(g(n))\) if \(g(n) = \Oh{f(n)}\). When \(f(n) = \Omega(g(n))\), we say that “\(f\) grows at least as fast as \(g\)”.
\(f(n) = \Theta(g(n))\) if \(f(n) = \Oh{g(n)}\) and \(g(n) = \Oh{f(n)}\). In such a case, we say that “\(f\) and \(g\) grow at the same rate”.

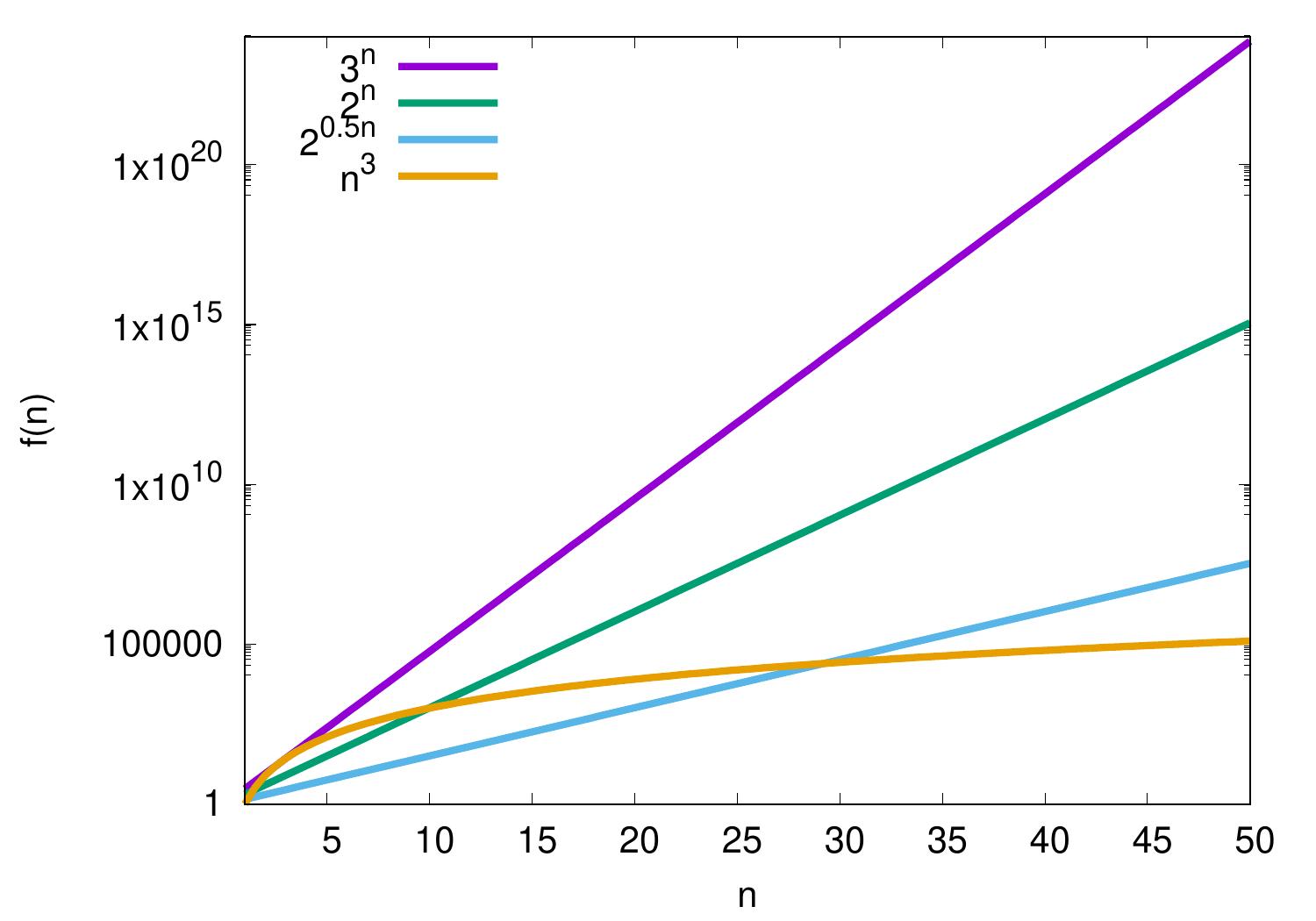
Example: Some functions

The plot below shows some functions. Please observe the logarithmic \(f(n)\) scale — compared to the linear scale, it allows easier visual comparison of different functions with orders of magnitude difference in values. In addition, is there is a constant difference between two graphs in logarithmic scale, then there is a constant factor difference between the corresponding values.

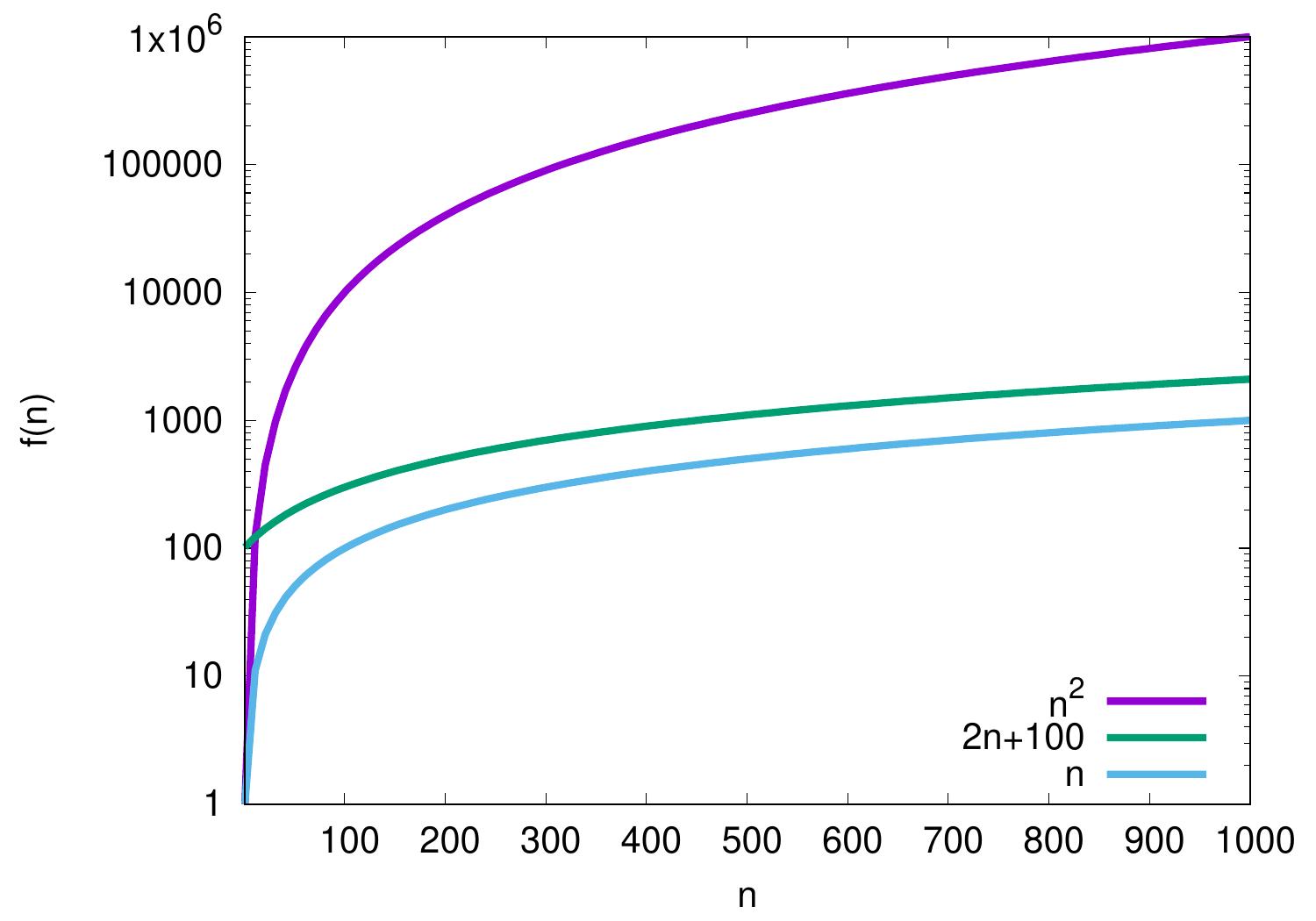
Based on the plot, it seems that the functions \(n\) and \(2n+100\) grow at the same rate when we consider large enough values of \(n\) because the difference between their graphs seems to approach a constant. Let’s study this in the \(\BigOh\) notation.
- \(n = \Oh{2n+100}\) as \(n \le 1(2n+100)\) for all \(n \ge 1\), and
- \(2n+100 = \Oh{n}\) as \(2n+100 \le 3n\) for all \(n \ge 100\).
Thus \(2n+100 = \Theta(n)\) and the functions grow at the same rate.
On the other hand, the difference between the graphs of \(n\) and \(n^2\) seems to increase when \(n\) grows. Let’s see what we can say with the \(\BigOh\) notation.
- \(n = \Oh{n^2}\) as \(n \le 1n^2\) for all \(n \ge 1\). Thus \(n\) grows at most as fast as \(n^2\).
- But \(n^2 \neq \Oh{n}\) because for all constants \(c,n_0 > 0\) it holds that \(n^2 > cn\) when \(n > \max\{c,n_0\}\).
In the same way, the difference between the graphs of \(2n+100\) and \(n^2\) seems to increase when \(n\) grows, although for small values of \(n\) we have that \(n^2 < 2n+100\). In the \(\BigOh\) notation we have that
- \(2n+100 = \Oh{n^2}\) as \(2n+100 \le 1n^2\) for all \(n \ge 12\). Thus \(2n+100\) grows at most as fast as \(n^2\).
- But \(n^2 \neq \Oh{2n+100}\) because, for \(n^2 \le c(2n+100)\) to hold for some constant \(c > 0\) when \(n\) grows, the value of the fraction \(\frac{n^2}{2n+100}\) should be bounded from above when \(n\) grows towards infinity, and this is not the case.

Note that the notation “\(=\)” above is not the usual equality but abuse of notation. The notation \(f(n) \in \Oh{g(n)}\) would be mathematically more precise when \(\Oh{g(n)}\) is seen as the set of functions that grow at most as fast as \(f(n)\). Thus, for instance, writing \(\Oh{g(n)} = f(n)\) is not allowed. For more discussion, please see Wikipedia.

There are also “little-o” and “little omega”, although their use is less common.

Definition

For two functions \(f\) and \(g\), we write \(f(n) = o(g(n))\) if for every constant \(c > 0\) there is a constant \(n_0 > 0\) such that \(f(n) < cg(n)\) for all \(n \ge n_0\).

If \(f(n) = o(g(n))\), “\(f\) grows slower than \(g\)”. We write \(f(n) = \omega(g(n))\) if \(g(n) = o(f(n))\) and say that “\(f\) grows faster than \(g\)”.

Some typical function families encountered in practise:

\(\Oh{1}\) — constant
\(\Oh{\log n}\) — logarithmic
\(\Oh{n}\) — linear
\(\Oh{n \log n}\) — linearithmic, “n log n”. Observe that \(\Oh{\log n!} = \Oh{n \log n}\).
\(\Oh{n^2}\) — quadratic
\(\Oh{n^3}\) — cubic
\(\Oh{n^k}\) — polynomial, \(k \ge 0\)
\(\Oh{c^n}\) — exponential, \(c > 1\)
\(\Oh{n!}\) — factorial

Constant, logarithmic, linear, linearithmic, quadratic, and cubic functions are all polynomial functions. We use base-2 logarithms unless otherwise stated but, in the context of O-notation, this is usually not relevant as \(\log_c n = \frac{\log_2 n}{\log_2 c}\) for any \(c > 1\) and \(\log_2 c\) is a constant when \(c\) is a constant.

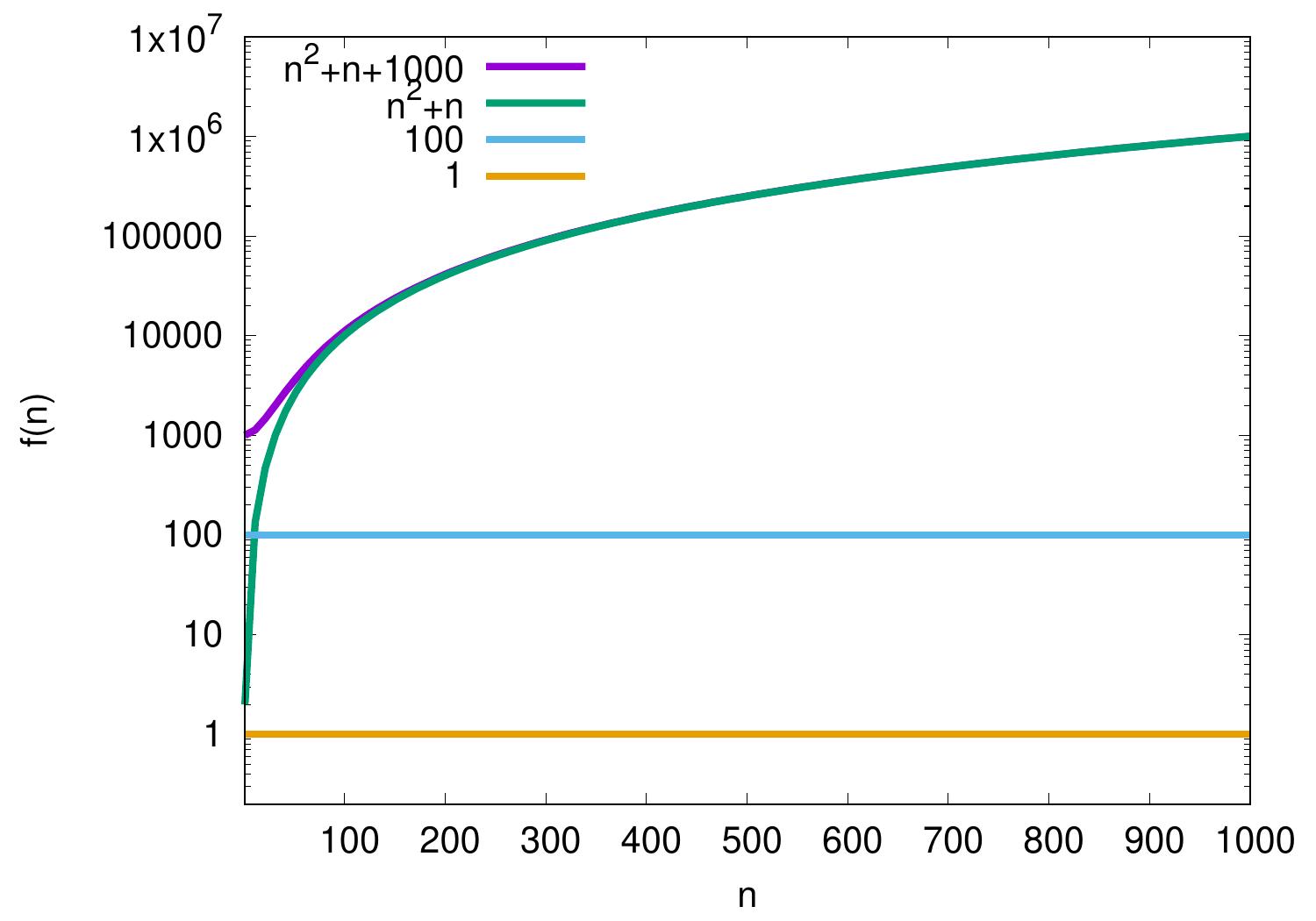
Example: Additive constants

Additive constants are irrelevant in \(\BigOh\) notation as we consider asymptotic growth rate of functions. For instance,

\(100 = \Oh{1}\) as for all \(n \ge n_0 = 1\) it holds that \(100 \le 100 \times 1\).
\(n^2 + n + 1000 = \Oh{n^2+n}\) as \(n^2 + n + 1000 \le 2(n^2+n)\) for all \(n \ge n_0 = 32\).

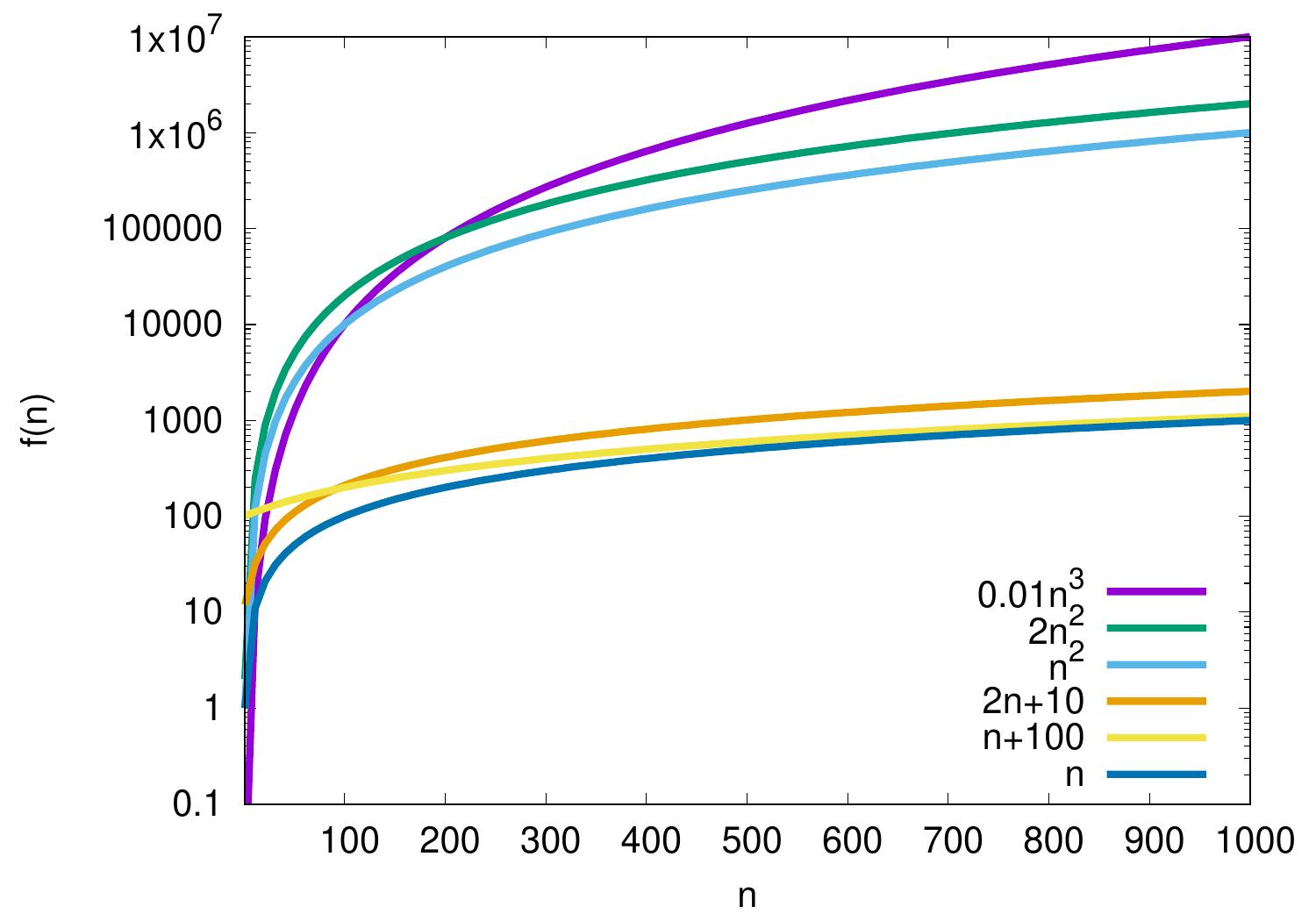
Example: Polynomials

In polynomials, the largest degree determines the growth rate. Some examples:

\(2n+10 = \Oh{n}\) as \(\frac{2n+10}{n}=2+\frac{10}{n} \le 3\) when \(n \ge 10\) and thus \(2n+10 \le 3n\) for all \(n \ge n_0 = 10\).
\(n^2 = \Oh{0.01n^3}\) as \(\frac{n^2}{0.01n^3} = \frac{100}{n} \le 1\) when \(n \ge 100\), and thus \(n^2 \le 0.01n^3\) for all \(n \ge n_0 = 100\).
\(0.01n^3 \neq \Oh{n^2}\) because for all \(n_0, c > 0\), we can choose \(n > \max\{100c,n_0\}\) and have that \(0.01n^3 > cn^2\).

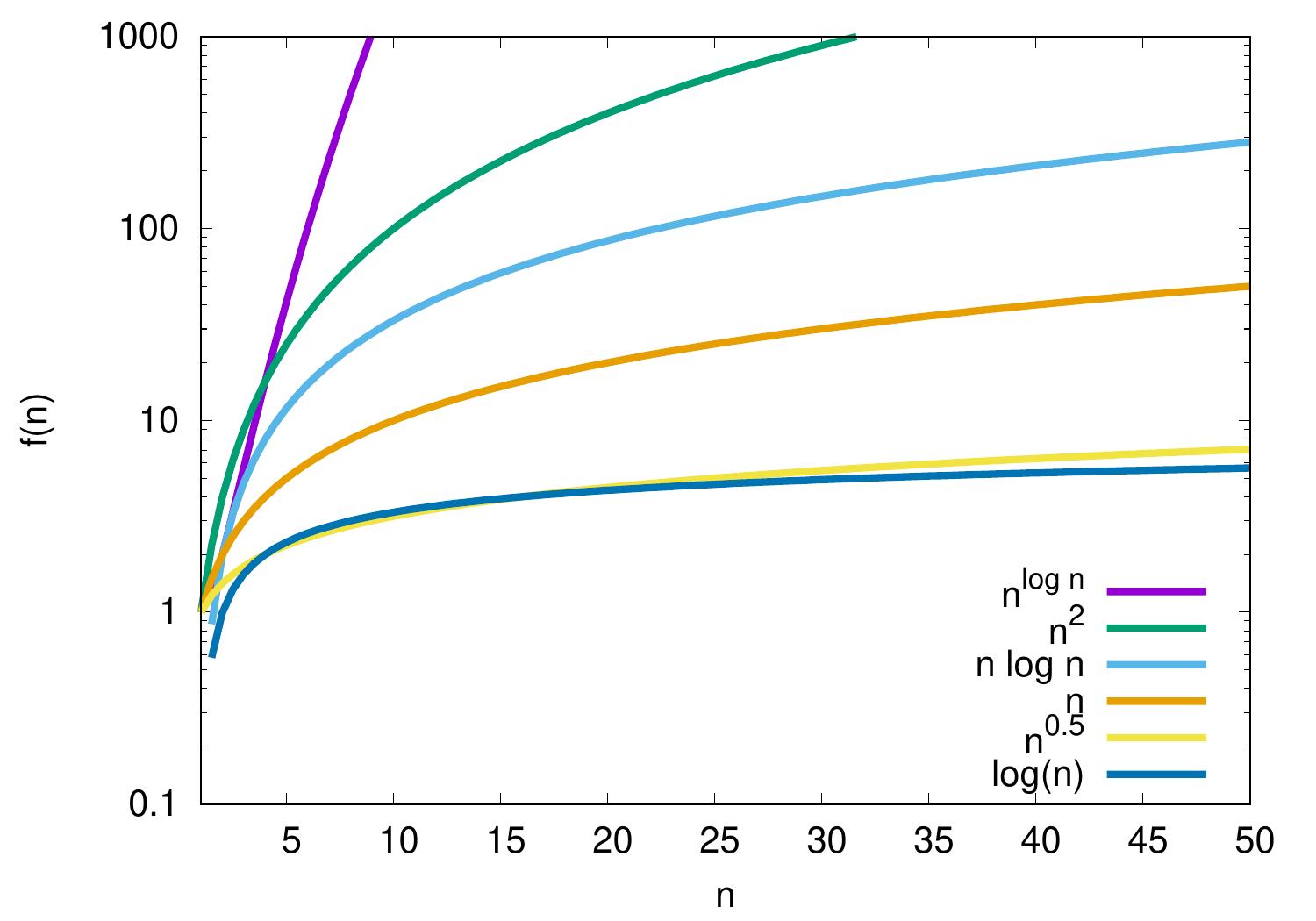
Example: Logarithms

The logarithmic function \(\log n\) grows rather slow but faster than any constant. It grows slower than any polynomial \(n^k\), where \(k > 0\) is a constant.

\(\log n = \Oh{n}\) but \(n \neq \Oh{\log{n}}\)
\(\log n = \Oh{\sqrt{n}}\) but \(\sqrt{n} \neq \Oh{\log{n}}\)
\(n \log n = \Oh{n^2}\) but \(n^2 \neq \Oh{n \log{n}}\)
\(n^2 = \Oh{n^{\log n}}\) but \(n^{\log n} \neq \Oh{n^2}\)
\(\log(10n) = \Oh{\log n}\) as \(\log(10n) = \log 10 + \log n\), please see Wikipedia for more logarithmic identities.

Example: Exponential functions

Exponential functions grow faster than polynomials. That is, \(c^n\) grows faster than \(n^k\), where \(c > 1\) and \(k > 0\) are constants. The base matters: for instance, \(2^n = \Oh{3^n}\) but \(3^n \neq \Oh{2^n}\). Constant factors in the exponent also matter because, for instance, \(2^{cn} = (2^c)^n\) for a constant \(c > 0\). But notices that in running-time analysis of algorithms, functions of the form \(2^{n^k}\), where \(k\) is a constant, are also commonly called exponential functions.

Running times of algorithms

Definition

The worst-case running time of a program/algorithm is \(\Oh{f(n)}\) if \(g(n) = \Oh{f(n)}\), where the function \(g(n)\) is obtained by taking, for each \(n\), the longest running time of any input of size \(n\).

When we say “a program/algorithm runs in time \(\Oh{f(n)}\)”, we usually mean that its worst-case running time is \(\Oh{f(n)}\). Similarly for the \(\Theta\) and \(\Omega\) notations. In addition to worst-case running time, one may also consider

the best-case running time obtained by taking the smallest running times for each \(n\), and
the average-case running time by taking the mean of the running times for each \(n\) over some set of inputs (usually all valid inputs).

Example: Linear search

Consider the simple linear search algorithm with the following input/output specification:

Input: an unordered array \(A\) of \(n\) elements and an element \(e\)
Output: does \(e\) appear in \(A\)?

In pseudo-code, one may express the algorithm as follows.

// Search for the element \(e\) in the array \(A\)
linear-search(\(A\), \(e\)):
  for \(i \in [1..\ALengthOf{A}]\):
    if \(A[i] \Eq e\): return true
  return false

Assume that array accesses and element comparisons are constant time operations.

The worst-case running time is \(\Theta(n)\). This occurs when the element is not included in the array. In this case, the whole for-loop is executed. In each loop body iteration, some constant amount \(c\) of time is spent in its instructions (array access, comparison, loop index increase). At the end, “false” is returned in some constant time \(d\). Thus the running time is \(\Theta(nc+d)=\Theta(n)\).
The best-case running time is \(\Theta(1)\) as \(e\) can be the first element in the array. In this case, only one array access and one comparison operation are performed.

Example: Straightforward multiplication of \(n \times n\) square matrices

Consider two \(n \times n\) matrices \((a_{ij})\) and \((b_{ij})\) with \(1 \le i,j \le n\). The method * in the Scala code below computes the \(n \times n\) product matrix

\[c_{ij} = \sum_{k=1}^n a_{ik} b_{kj}\]

class Matrix(val n: Int):
  require(n > 0, "n must be positive")
  val entries = new Array[Double](n * n)
  /** Access elements with "m(i,j)" */
  def apply(row: Int, column: Int) =
    entries(row * n + column)

  /** Set elements with "m(i,j) = v" */
  def update(row:Int, col:Int, v:Double) =
    entries(row * n + col) = v

  /** Get the product of this and that */
  def *(that: Matrix): Matrix =
    require(n == that.n)
    val result = Matrix(n)
    for r <- 0 until n; c <- 0 until n do
      var v = 0.0
      for i <- 0 until n do
        v += this(r, i) * that(i, c)
      result(r, c) = v
    result

Let’s analyze the asymptotic running time of the multiplication method *.

Initializing the result matrix takes \(\Theta(n^2)\) steps: the \(n \times n\) matrix is allocated, and each entry in it is initialized to have the value \(0\).
The outer loop iterates row from \(0\) to \(n-1\). Thus its body is executed \(n\) times.
Inside the body of the outer loop, the middle loop iterates column from \(0\) to \(n-1\). Thus its body is executed \(n\) times.
Finally, the inner loop iterates i from \(0\) to \(n-1\) as well.
Inside the inner loop, the floating point number multiplication and array accesses are constant time operations.
Because of the above four items, the for-loops part takes \(\Theta(n^3)\) time.

To sum up, the running time of the * method is \(\Theta(n^2+n^3) = \Theta(n^3)\).

Recursion and Recurrences

For recursive programs, it can be more difficult to analyze the asymptotic running time directly from the (pseudo)code.

Example: Binary search (recursive version)

From the CS-A1120 Programming 2 course, recall the binary search algorithm for searching an element in a sorted array, implemented below in Scala.

def binarySearch[T](arr: Array[T], e: T)(using ord: Ordering[T]) =
  def inner(lo: Int, hi: Int): Boolean =
    if lo <= hi then
      val mid = lo + ((hi - lo) / 2)
      val cmp = ord.compare(e, arr(mid))
      if cmp == 0 then true                 // e == arr(mid)
      else if cmp < 0 then inner(lo, mid-1) // e < arr(mid)
      else inner(mid+1, hi)                 // e > arr(mid)
    else
      false
  inner(0, arr.length-1)

But in fact analyzing corresponding iterative versions may not be easier either. For instance, consider the iterative version of the binary search algorithm below.

def binarySearch[T](arr: Array[T], e: T)(using ord: Ordering[T]): Boolean =
  var lo = 0
  var hi = arr.length - 1
  while lo <= hi do
    val mid = lo + ((hi - lo) / 2)
    val cmp = ord.compare(e, arr(mid))
    if cmp == 0 then
      return true // e == arr(mid)
    else if cmp < 0 then
      hi = mid-1  // e < arr(mid)
    else
      lo = mid+1  // e > arr(mid)
  return false

To obtain an asymptotic running time estimate for recursive programs, one can try to formulate the running time (or some other measure) \(T(n)\) on inputs of size \(n\) as a recurrence equation of form

\[T(n) = ...\]

where

\(n\) is some parameter usually depending on the (current) input size, and
the right hand side recursively depends on the running time(s) \(T(n')\) of some smaller values \(n'\) and some other terms.

In addition, the base cases, usually \(T(0)\) or \(T(1)\), not depending on other \(T(n')\) need to be given. One then solves the equation somehow. Note that \(T(n)\) is not the value that the function computes but the number of steps taken when running the algorithm on an input of size \(n\).

Example: Recurrence for binary search

Consider again the recursive binary search program below.

def binarySearch[T](arr: Array[T], e: T)(using ord: Ordering[T]) =
  def inner(lo: Int, hi: Int): Boolean =
    if lo <= hi then
      val mid = lo + ((hi - lo) / 2)
      val cmp = ord.compare(e, arr(mid))
      if cmp == 0 then true                 // e == arr(mid)
      else if cmp < 0 then inner(lo, mid-1) // e < arr(mid)
      else inner(mid+1, hi)                 // e > arr(mid)
    else
      false
  inner(0, arr.length-1)

The recursive part considers sub-arrays of size \(n\), where \(n\) equals to hi - lo + 1 in our implementation above.

If \(n \le 0\), the recursion terminates with “false”.
If \(n \ge 1\), a comparison is made and
- the search either terminates with “true” (the element was found) or
- the same recursive function is called with a sub-array of size at most \(\lfloor n/2 \rfloor\).

Assuming that array accesses and element comparisons are constant-time operations, we thus get the recurrence equations

\[T(0) = d \text{ and } T(n) = c + T(\lfloor n/2 \rfloor)\]

where \(d\) and \(c\) are some constants capturing the running time taken to compare the bounds, array access, element comparison and so on. Here \(T(n)\) is a worst-case upper bound for the running time on arrays with \(n\) elements. This is because we have omitted the early termination case in which the element is found, but assume that the recursion always runs until the base case of arrays of length 0.

Let’s solve the recurrence equations

\[T(0) = d \text{ and } T(n) = c + T(\lfloor n/2 \rfloor)\]

In this case, we obtain an upper bound by considering inputs of length \(n = 2^k\) for some non-negative integer \(k\). Now

\[T(2^k) = c + T(2^{k-1}) = c + (c + T(2^{k-2})) = ... = k c + T(2^{0}) = c (k+1) + d.\]

As \(n = 2^k\) implying \(k = \Lg n\), and \(c\) and \(d\) are constants, we get

\[T(n) = T(2^k) = c k + c + d = c \Lg n + c + d = \Oh{\Lg n}.\]

When \(n\) is not a power of two, \(T(n) \le T(2^{\lceil \Lg n\rceil}) = c \lceil \Lg n\rceil + 2c + d = \Oh{\Lg n}\) as \(T(n)\) is monotonic.

When using the \(\BigOh\)-notation, constants can be usually eliminated already in the beginning by replacing them with \(1\). In our binary search example, the recurrence is thus

\[T(0) = 1 \text{ and } T(n) = 1 + T(\lfloor n/2 \rfloor)\]

Solving this gives again \(T(n) = \Oh{\Lg n}\). Sometimes one also writes

\[T(0) = \Oh{1} \text{ and } T(n) = \Oh{1} + T(\lfloor n/2 \rfloor).\]

In addition to the number of instructions taken, we may sometimes be interested in some other aspects of the algorithm. For instance, if we know that comparisons are very expensive, we may analyze how many of them are taken in a search or sorting algorithm.

Example

For binary search, an asymptotic upper bound for the number of comparisons made on an input of elements \(n\) can be obtained again by the recurrence

\[T(0) = T(1) = 1 \text{ and } T(n) = T(\lfloor n/2 \rfloor) + 1\]

and thus \(T(n) = \Oh{\Lg n}\).

We’ll see slightly more complex recurrences later when analyzing sorting algorithms.

Example: The subset sum problem

Consider the subset sum problem:

Given a set \(S = \Set{v_1,...,v_n}\) of integers and a target integer \(t\). Is there a subset \(S'\) of \(S\) such that \(\sum_{v \in S'}v = t\)?

Below is a (very simple) recursive Scala program solving it:

def subsetsum(s : List[Int], t : Int) : Option[List[Int]] =
  if t == 0 then
    Some(Nil)  // Sum of zero elements is 0
  else if s.isEmpty then
    None  // Cannot obtain t != 0 with zero elements
  else
    // Do not include the first element in the solution
    val solNotIncluded = subsetsum(s.tail, t)
    if solNotIncluded.nonEmpty then
      solNotIncluded
    else
      // Include the first element in the solution
      val solIncluded = subsetsum(s.tail, t-s.head)
      if solIncluded.nonEmpty then
        Some(s.head :: solIncluded.get)
      else
        // No subset of s can sum to t
        None

Let’s form a recurrence for the running time of the recursive program with the parameter \(n\) being the size of the set. In the worst-case scenario, there is no solution and the recursion terminates only when the set is empty. In each call, the program makes some constant-time tests etc and then two recursive calls with a set that has one element removed. Thus we get the recurrence

\[T(0) = 1 \text{ and } T(n) = 1 + T(n-1) + T(n-1) = 1 + 2T(n-1)\]

Expanding the recurrence, we get

\begin{eqnarray*} T(n) &=& 1 + 2T(n-1)\\ &=& 1 + 2(1+2T(n-2))\\ &=& 1 + 2 + 4(1 + 2T(n-3))\\ &=& ... \\ &=& \sum_{i=0}^n 2^i\\ &=& 2^{n+1}-1 \\ &=& \Theta(2^{n}) \end{eqnarray*}

Thus the algorithm takes exponential time in the worst case.

In the (very rare) best case, the target equals to \(0\) and the program takes constant time to complete.