Experimental analysis

The O-notation described earlier disregards constant factors. In practice, however, constant factors in running times and other resource usages do matter. In addition to mathematical analysis, we may thus perform experimental performance analysis. For instance, we may

take implementations of two algorithms that perform the same task,
run these on the same input set, and
compare their running times.

Similarly, we may

instrument the code, for instance, to count all the comparison operators made and then run the algorithm on various inputs to see how many comparisons are made on average or in the worst case, or
use some profiling tool (such as valgrind for C++ programs) to find out numbers of cache misses.

Example: Square matrix multiplication

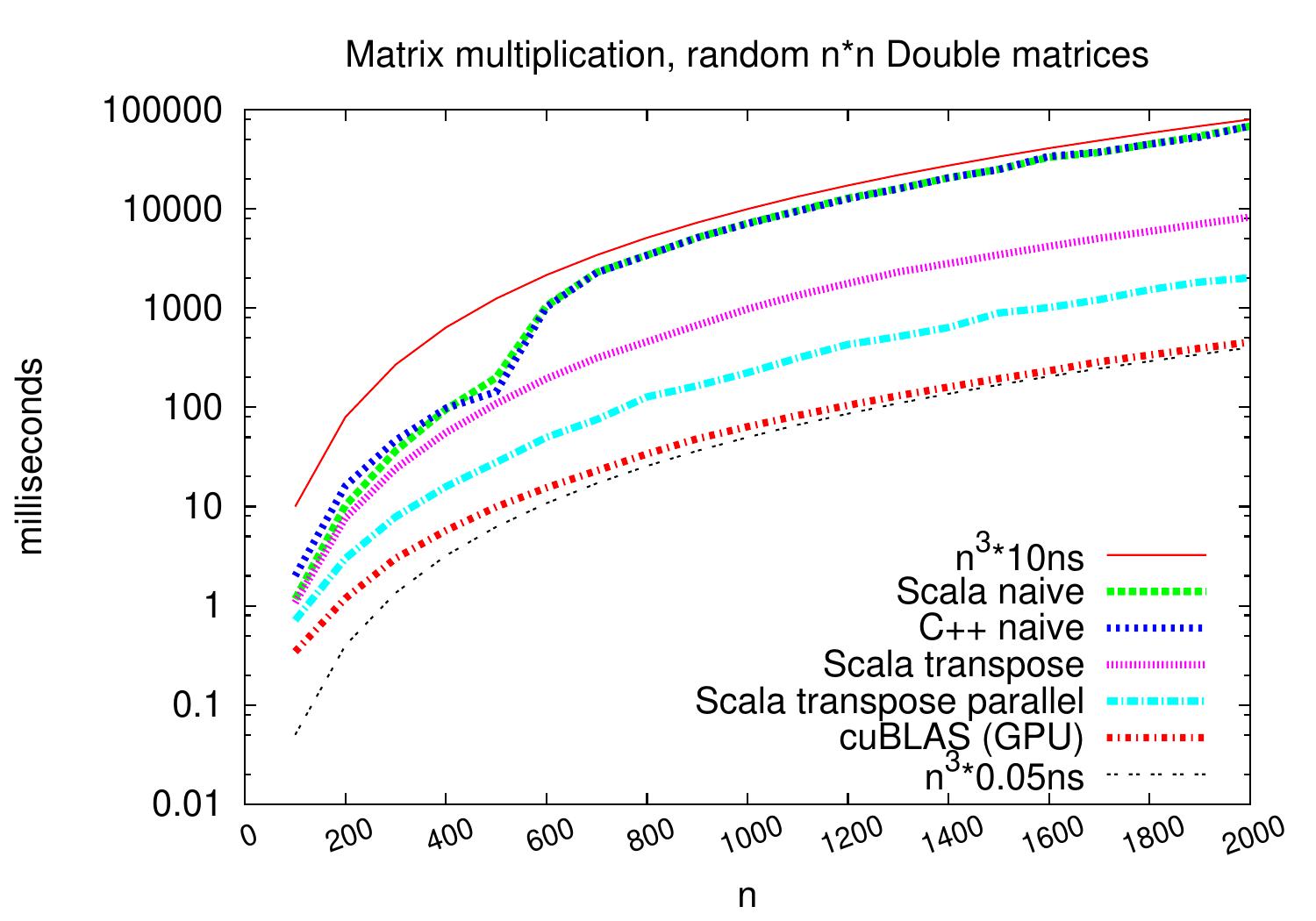
Let’s compare the performance of some \(n \times n\) matrix multiplication implementations:

Scala naive: the code in the Running times of algorithms section
C++ naive: the same in C++
Scala transpose: transpose the other matrix for better cache behavior
Scala transpose parallel: the previous but use 8 threads of a 3.20GHz Intel Xeon(R) E31230 CPU
cuBLAS (GPU): use NVIDIA Quadro 2000 (a medium range graphics processing unit) and a well-designed implementation in the NVIDIA cuBLAS library (version 7.5)

The plot below shows that the implementations scale similarly. But on \(2000 \times 2000\) matrices, on this particular machine, the running times drop from the \(68\mathrm{s}\) of the naive algorithm to \(0.45\mathrm{s}\) of the GPU algorithm. Thus, in practice, constant factors can make a large difference.

Simple running time measurement in Scala

As seen in the CS-A1120 Programming 2 course, we can measure running times of functions quite easily in Scala.

object timer:
  val bean = java.lang.management.ManagementFactory.getThreadMXBean()
  def getCpuTime = if bean.isCurrentThreadCpuTimeSupported() then
    bean.getCurrentThreadCpuTime() else 0

  /* Execute and measure the single-thread running time of f.
   * Does NOT measure running times of parallel programs correctly. */
  def measureCpuTime[T](f: => T): (T, Double) =
    val start = getCpuTime
    val r = f
    val end = getCpuTime
    (r, (end - start) / 1e9)

  /* Execute and measure the wall-clock running time of f. */
  def measureWallClockTime[T](f: => T): (T, Double) =
    val start = System.nanoTime
    val r = f
    val end = System.nanoTime
    (r, (end - start) / 1e9)

Observe that wall clock times (the function measureWallClockTime) should be used when measuring running times of parallel programs. This is because the method getCurrentThreadCpuTime used in measureCpuTime measures the CPU time of only one thread — this thread may be, for instance, the one that initiates the real parallel computations and then just waits for the other threads to finish.

Unfortunately, things are not always that simple. Let’s run the following code which sorts 100 arrays of 10000 integers:

@main def test() =
  import timer._
  val rand = util.Random()
  val times = collection.mutable.ArrayBuffer[Double]()
  for test <- 0 until 100 do
    // Make an array of 10000 random integers
    val a = Array.fill[Int](10000)(rand.nextInt)
    // Sort the array and measure the running time
    val (dummy, t) = measureCpuTime { a.sorted }
    times += t
  println("Running times: "+times.map(t => f"${t*1e3}%.3fms").mkString(", "))

An output of the program:

Running times: 2.093ms, 0.588ms, 0.601ms, 0.591ms, 0.583ms, 0.576ms, 0.584ms, 0.588ms, 0.581ms, 0.625ms, 0.582ms, 0.587ms, 0.583ms, 0.633ms, 0.612ms, 0.608ms, 0.599ms, 0.591ms, 0.602ms, 0.586ms, 0.593ms, 0.626ms, 0.582ms, 0.585ms, 0.599ms, 0.598ms, 0.610ms, 0.618ms, 0.645ms, 0.666ms, 0.672ms, 0.642ms, 0.734ms, 0.657ms, 0.669ms, 0.687ms, 0.671ms, 0.640ms, 0.702ms, 0.681ms, 0.646ms, 0.700ms, 0.655ms, 0.665ms, 0.634ms, 0.696ms, 0.668ms, 0.685ms, 0.694ms, 0.699ms, 0.711ms, 0.724ms, 0.706ms, 0.690ms, 0.735ms, 0.690ms, 0.669ms, 0.703ms, 0.644ms, 0.629ms, 0.643ms, 0.658ms, 0.659ms, 0.679ms, 0.669ms, 0.682ms, 0.709ms, 0.663ms, 0.686ms, 0.662ms, 0.696ms, 0.659ms, 0.661ms, 0.669ms, 0.649ms, 0.676ms, 0.485ms, 0.406ms, 0.405ms, 0.450ms, 0.479ms, 0.458ms, 0.414ms, 0.441ms, 0.430ms, 0.422ms, 0.429ms, 0.425ms, 0.428ms, 0.438ms, 0.429ms, 0.424ms, 0.426ms, 0.437ms, 0.432ms, 0.441ms, 0.420ms, 0.430ms, 0.427ms, 0.431ms

The program measures the same code on similar inputs but the running times improve significantly after some repetitions. Why is this happening? The above behaviour can be explained as follows.

A Scala program is first compiled into Java bytecode.
The resulting Java bytecode is executed in a Java virtual machine (JVM).
The execution may start in interpreted mode.
After while, some parts of the program can then be just-in-time compiled to native machine code during the execution of the program.
The compiled code may then be globally optimized during the execution.
In addition, garbage collection may happen during the execution.

As a consequence, when measuring running times of programs with shortish running times, one should be careful when interpreting the results. But for programs with larger running times this is usually not so big problem.

As shown above, reliably benchmarking programs written in interpreted, virtual machine based, garbage-collected languages (such as Java, Scala and Python) can be non-trivial, especially if the running times are small. In addition to adhoc execution repetition described above, one can also use benchmarking tools such as

which automate many aspects in benchmarking. For the challenges and techniques of reliable benchmarking, an interested reader can see, for instance,

A. Georges et al: Statistically rigorous Java performance evaluation, Proc. OOPSLA 2007, pp. 57-76.