Intro: small key universe, bit sets and direct-access tables¶

Before introducing hashing and hash tables, let us first assume that

the number $ m $ of all possible keys is small, and
the keys are, or can be easily mapped to, the integers $ [0..m-1] $.

In this case, it is easy to implement sets and maps so that the operations insert, search, and remove take constant time.

Bit sets¶

When the keys are, or have been mapped to, the integers $ [0..m-1] $, a simple way to implement a mutable set data structure for them is to use a bit set (also called bit array or bit vector):

Allocate an array $ a = a_0 a_1 … a_{M-1} $ of $ M = \Ceil{\frac{m}{8}} $ 8-bit bytes.
A key $ k \in [0..m-1] $ is in the current set if and only if the bit $ k \bmod 8 $ in the byte $ a_{\Floor{k/8}} $ is $ 1 $.

Now it should be obvious how to implement the operations insert, search, and remove with bit manipulation operations so that they operate in constant time (recall this section in the Programming 2 notes).

Example

The bit set below stores a subset of the keys $ \Set{0,1,…,999} $. The underlying array data structure has of 125 bytes. Now the keys $ 0 \times 8+1=1 $, $ 0 \times 8+4=4 $, $ 100 \times 8+6=806 $, $ 124 \times 8+7=999 $ are included in the current set, while the key $ 100 \times 8+5=805 $ is not.

Bit sets are a very memory efficient way of representing dense sets (meaning sets in which a large portion of the keys are included). For sparse sets space is “wasted” and, for instance, listing all the keys in the set becomes costly.

Some implementations of bit sets in standard libraries:

BitSet in Scala
bitset in the C++ standard library

Direct-access tables¶

Again, suppose that we have a small set of $ n $ possible keys and that the set can be easily mapped to the integers $ [0..m-1] $. In that case, building a map/dictionary from the keys to some value type is easy; just allocate an array of $ m $ elements and store the value of the key $ i $ in the index $ i $ of the array.

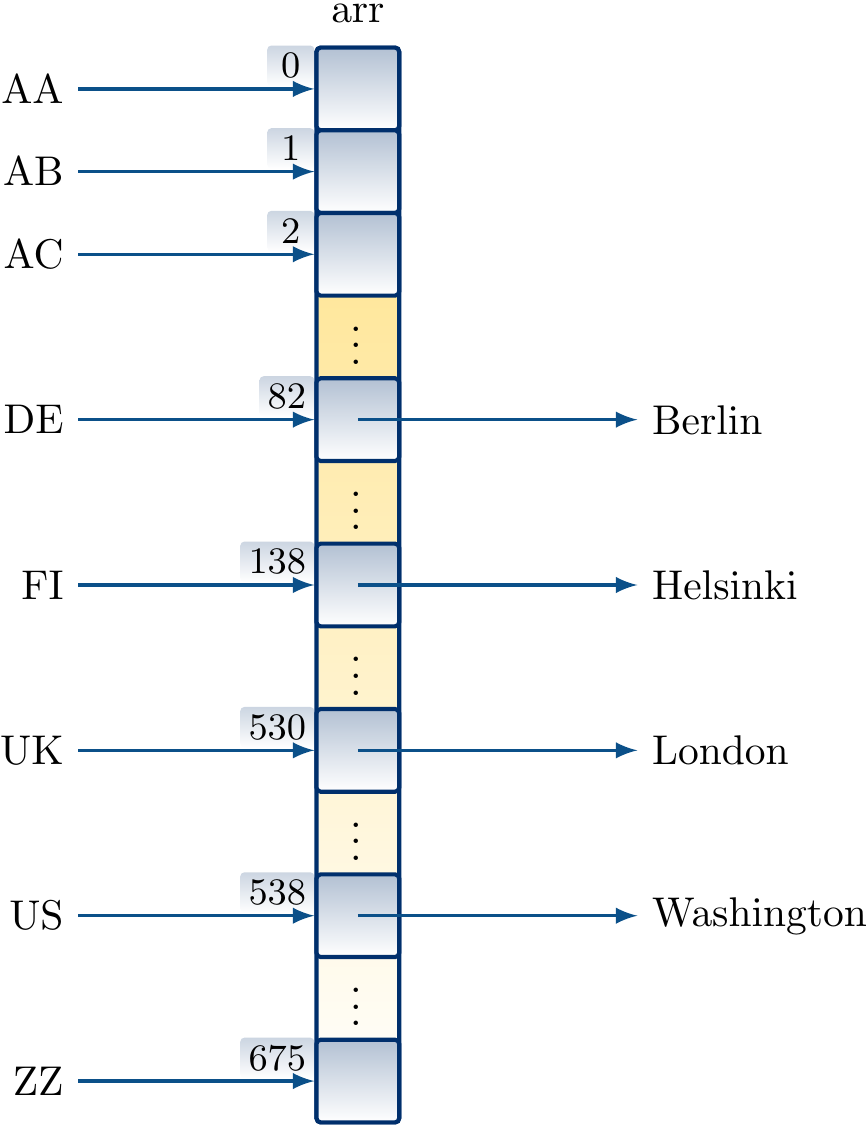
For instance, in the two-letter country codes in ISO 3166-1 alpha-2 drawn from the alphabet $ \Set{\textrm{A},\textrm{B},…,\textrm{Z}} $ of 26 letters, there are $ 26 \times 26=676 $ possible codes. Of these 249, such as FI and UK, are actually assigned to some meaning. We can implement a dictionary mapping country codes to objects, such as capital city names, by having a direct-access table with 676 entries. The value $ v $ corresponding to a code $ c_1 c_2 $ is simply stored in the entry $$\mathit{index}(c_1 c_2) = 26 f(c_1) + f(c_2)$$ of the array, where $ f(\textrm{A})=0,f(\textrm{B})=1,…,f(\textrm{Z})=25 $.

Example

Mapping country codes to the entries in a direct-access table arr:

It is now easy to implement the insert, search, and remove operations to run in constant time. As an example, one can implement a country code map in Scala as follows:

import scala.reflect.ClassTag
class CountryMap[B >: Null]()(implicit tag: ClassTag[B]) {
  private val arr = new Array[B](676)
  private def f(c: Char) = c.toInt-'A'.toInt
  private def isValidCode(code: String) = code.length == 2 &&
    0 <= f(code(0)) && f(code(0)) < 26 &&
    0 <= f(code(1)) && f(code(1)) < 26
  def index(code: String): Int = {
    require(isValidCode(code))
    f(code(0))*26 + f(code(1))
  }
  def apply(code: String): Option[B] = {
    val v = arr(index(code))
    if(v == null) None else Some(v)
  }
  def update(code: String, value: B) = {
    require(value != null)
    arr(index(code)) = value
  }
  def remove(code: String) = {
    arr(index(code)) = null
  }
}

Note: use of null pointers is generally discouraged in Scala (use Option instead) but excusable inside data structure implementations. Extending the class with a constant-time size operation, returning the number of the keys in the map, is easy as well: how would you implement it?

Example

Building a direct-access table mapping country codes to some capital city names.

val capital = new CountryMap[String]()
capital("DE") = "Berlin"
capital("FI") = "Helsinki"
capital("UK") = "London"
capital("US") = "Washington"
println(capital("FI"))

produces

Some(Helsinki)

Graphically the data structure after the insertions could be illustrated as below.