Round 10: Computationally more difficult problems
So far almost all of our algorithms have been rather efficient, having worst-case running times such as \(\Oh{\Lg{n}}\), \(\Oh{n}\), \(\Oh{n \Lg{n}}\), \(\Oh{(E + V)\Lg{V}}\) and so on. But there are lots of practical problems for which we do not know any efficient algorithms. In fact, there are even problems that provably cannot be solved by computers. Here “solve by computers” means “to have an algorithm that in all the cases gives the answer and the answer is correct”. The proof that such problems exists and more about this topic can be found in the Aalto course CS-C2160 Theory of Computation (5cr, periods III-IV).
Example
There is no algorithm that always decides whether a multivariate polynomial has integer-valued roots. For further discussion, see for instance
Bjorn Poonen: Undecidability in Number Theory, Notices of the AMS 33(5):344–350, 2008.
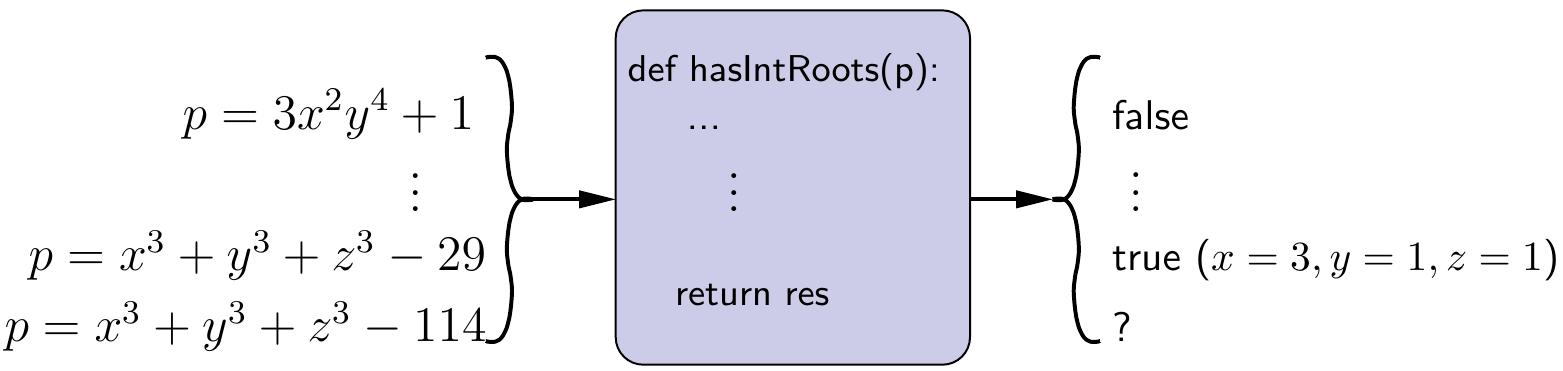
As a curiosity, the output to \(x^3+y^3+z^3-114\) is marked with “?” in the figure because we do not at the moment (May 2024) know whether the are integers \(x\), \(y\) and \(z\) such that \(x^3+y^3+z^3 = 114\). The cases 33 and 42 were solved only in 2019, see this Wikipedia article.
This round
gives a semi-formal description for one important class of computationally hard but still solvable problems, called NP-complete problems, and
provides some methods for attacking such problems in practice.
Definitions by using formal languages etc and most of the proofs are not covered, they are discussed more in the Aalto courses
CS-C2160 Theory of Computation, and
CS-E4530 Computational Complexity Theory.
Contents:
Material:
These notes
Chapter 34 in Introduction to Algorithms (Aalto access) on the abstraction level of these notes:
the formal language definitions are not required,
nor are the proofs that are not in the notes.
Further references:
Sanjeev Arora and Boaz Barak, Computational Complexity: A Modern Approach