Introduction: sets and maps
In this and the next round we are interested in the abstract data types for dynamic sets and maps. Here “dynamic” means that the elements, or key-value associations in maps, are inserted, searched for and removed all the time in an online fashion.
Sets
A basic API for a set abstract data type could be
insert(e)for inserting the elementein the set,
search(e)for finding whether the elementeis in the set, and
remove(e)for deleting the elementefrom the set.
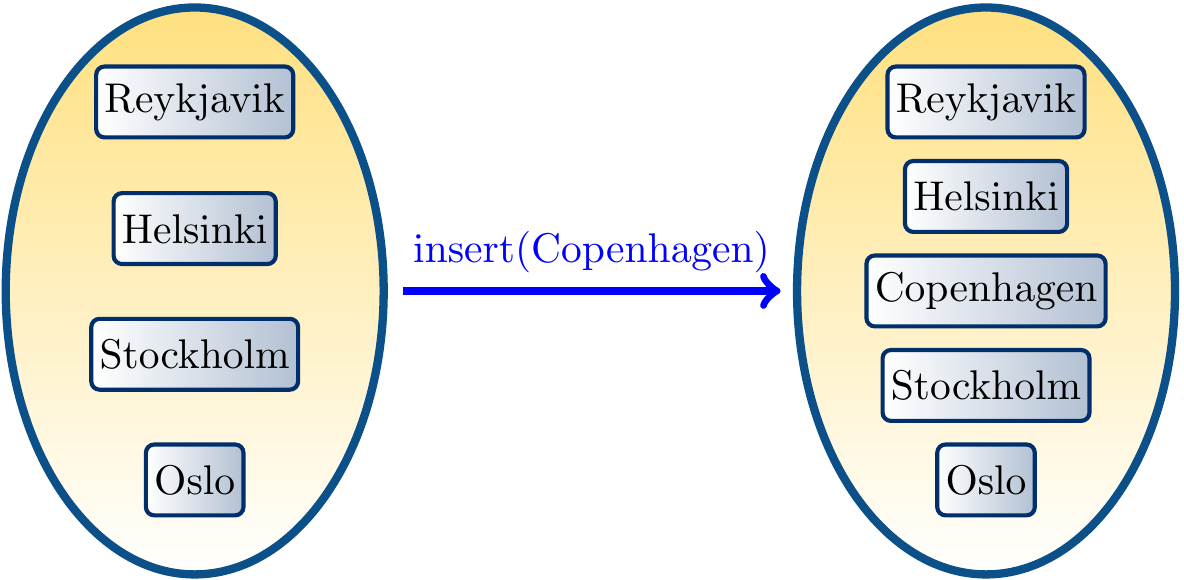
The figure below shows the set diagrams for two sets of strings, where the latter is obtained by inserting a new string in it.
In Scala, this API corresponds to the collection.mutable.Set trait, which is implemented, among others, in the mutable TreeSet and HashSet classes. The methods corresponding to the ones in the asbtract API are
s.add(e)ors += efor inserting an elementeinto the sets,
s.contains(e)ors(e)for checking whether the setscontains the elemente, and
s.remove(e)ors -= efor removing the elementefrom the sets.
In Java, the counterpart is the java.util.Set interface. In C++, the standard library contains two classes, set and unordered_set, implementing a variant of the API (the difference is explained below).
Maps
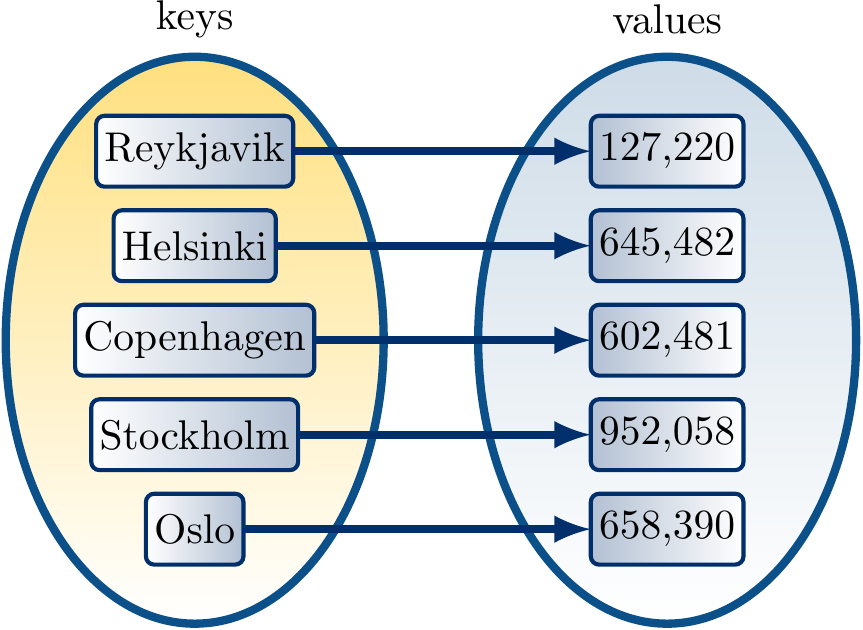
For maps, also called dictionaries in some programming languages, the API allows associating each key to a value.
In Scala collection.mutable.Map trait, the methods are called
m.update(k,v)or simplym(k) = vfor setting the value of the keyktovin the mapm,
m.apply(k)or simplym(k)for getting the value associated with the keykin the mapm, and
m.remove(k)for removing the keykfrom the mapm.
In the Java java.util.Map interface
the methods are called put, get, and remove.
In the C++ standard library map and unordered_map classes, the methods are called
insert, or simplym[k] = v, for a mapm, keyk, and valuev,
m.at(k), or simplym[k], and
m.erase(k).
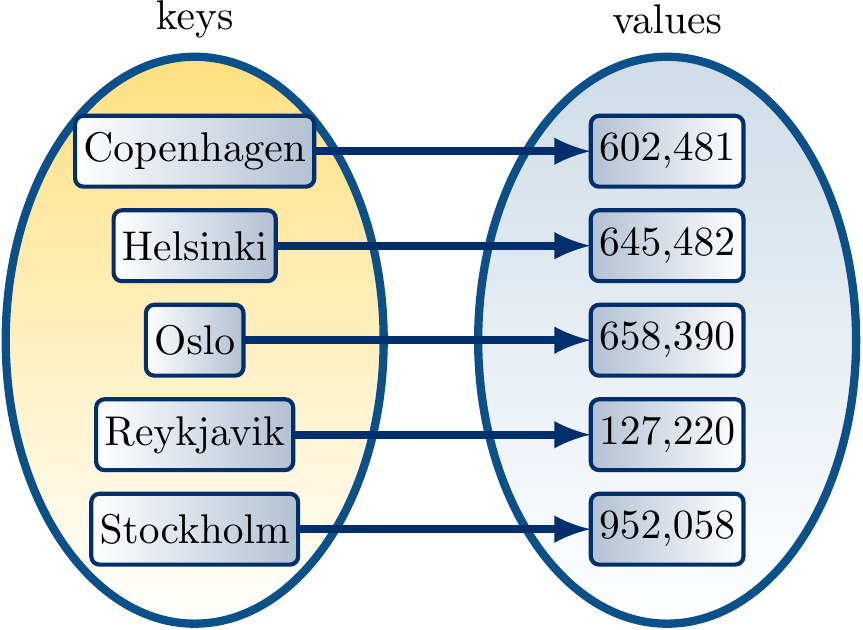
Ordered sets and maps
In this round, we will in fact consider ordered sets and ordered maps that
assume an ordering \(\le\) between the elements/keys, and
allow efficient searching for the smallest, next smallest, etc element/key.
The abstract API of ordered sets extends the basic API with
minfor getting the smallest element in the set,maxfor getting the largest element in the set,predecessor(e)for getting the largest element that is smaller thane, andsuccessor(e)for getting the smallest element that is larger thane.
Our goal is to have data structures and algorithms allowing the operations to be done in logarithmic time in the size of the set. Furthermore, the elements can be listed in ascending order in linear time. Note the difference to the priority queue API of the previous round (Section Priority queues with binary heaps): searching and removing arbitrary elements, as well as finding the minimum and successor elements, are now also supported.
Implementations in some programming languages:
In Scala, the TreeSet class implements a variant of the API allowing ordered iteration over the elements in the set. In the class,
headandfirstKeygive the smallest element, whilelastandlastKeyreturn the largest element. Similarly,maxBeforeandminAftergive the predecessor and successor elements.Some notes:
minandmaxare slow, linear time generic operations.In the current Scala version,
val s = collection.mutable.Set()creates a new “hash set” (covered in the next round) in which the ordering-based operations above take linear time in the worst case. Useval s = collection.mutable.TreeSet()to create an ordered set.
In Java, the java.util.TreeSet API is close to the abstract one:
firstgives the smallest element,
lastgives the largest element,
higher(e)gives the smallest element that is larger thane, and
lower(e)gives the largest element that is smaller thane.
The C++ standard library has the set class.
For maps, the corresponding classes are
TreeMap in Scala,
java.util.TreeMap in Java, and
map in the C++ standard library.