Dynamic programming¶

Dynamic programming is a generic algorithm design technique. It is applicable for solving many optimization problems, where we want to find the best solution for some problem. In a nutshell, dynamic programming could be described as “exhaustive recursive search with sub-problem solution reuse”. The term “dynamic programming” itself is due to historical reasons, see the text in this Wikipedia page.

The generic idea in dynamic programming is as follows.

Define the (optimal) solutions for the problem by using (optimal) solutions for some sub-problems of the original problem. This leads to a recursive definition for the (optimal) solutions.
Check if the sub-problems occur many times in the expansion of the recursive definition.
If they do, apply memoization when evaluating the recursive definition. That is, instead of recomputing the same sub-problems again and again, store their solutions in a map/table/etc and reuse the solutions whenever possible.

(If they don’t, the sub-problems don’t “overlap” and dynamic programming is not applicable. Sometimes it is possible to make an alternative recursive definition that has overlapping sub-problems.)

Let us now practise this proceduce by considering three increasingly complex problems and showing how they can be solved with dynamic programming.

Example I: Fibonacci numbers¶

Let’s start with a very simple example from previous courses. The Fibonacci numbers sequence $ F_n = 0,1,1,2,3,5,8,… $ is defined recursively by $$F_0 = 0, F_1 = 1, \text{ and } F_n = F_{n-1}+F_{n-2} \text{ for } n \ge 2$$ It is rather easy to implement a program that computes the $ n $th Fibonacci number by using recursion:

def fib(n: Int): BigInt = {
  require(n >= 0)
  if(n == 0) 0
  else if(n == 1) 1
  else fib(n-1) + fib(n-2)
}

The call tree, also called recursion tree, when computing fib(6):

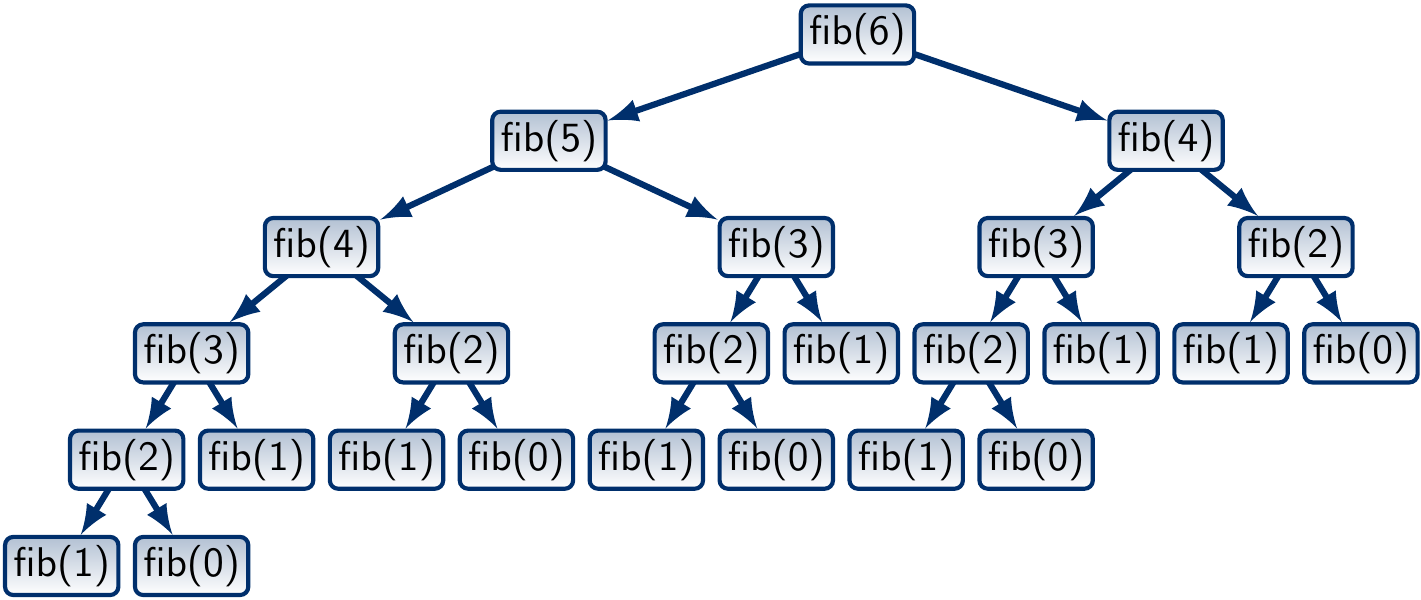
Observe that many (pure) function invocations occur multiple times. In other words, the same sub-problem fib(i) is solved many times. This is reflected in the running time, computing the 45th Fibonacci number 1134903170 takes almost 50 seconds on a rather standard desktop machine:

scala> measureCpuTime {fib(45) }
res2: (BigInt, Double) = (1134903170,49.203652944)

What is the asymptotic time-complexity of this algorithm? Assuming that addition of numbers could be done in constant time, we get the following recurrence: $$T(n) = T(n-2)+T(n-1)+\Oh{1}$$ For this we have some easy-to-obtain lower bounds:

$ T(n) \ge F_n = \frac{\varphi^n-(-\frac{1}{\varphi})^n}{\sqrt{5}} = \frac{\varphi^n}{\sqrt{5}}-\frac{(-\frac{1}{\varphi})^n}{\sqrt{5}} = \Omega(\varphi^n) $, where $ \varphi= 1.6180339887… $ is the golden ratio.
$ T(n) \ge 2 T(n-2) + \Oh{1} $ and thus $ T(n) = \Omega(2^{n/2}) $.

Therefore, the algorithm takes at least exponential time. The above analysis is actually not very precise because the addition is not done in constant time as the binary representations of the numbers in $ F_n $ grow linearly to $ n $. Therefore, the $ \Oh{1} $ term in the recurrence should be $ \Omega(n) $. Also note that $ n $ is the value of the argument, not its representation length. If we replace Int with BigInt and call the function with an argument number consisting $ m $ bits, the running time is $ \Omega(\varphi^{2^m}) $.

Applying dynamic programming¶

Instead of recomputing the values fib(i) over and over again, we can memoize the values in a map and reuse them whenever possible. In Scala, a basic version of memoization is easy to obtain by just using a mutable map that maps the sub-problems to their solutions (in this case, the map associates the argument i to the value fib(i)).

def fib(n: Int): BigInt = {
  require(n >= 0)
  val m = scala.collection.mutable.Map[Int, BigInt]() // ADDED
  def inner(i: Int): BigInt = m.getOrElseUpdate(i, {  // CHANGED
    if(i == 0) 0
    else if(i == 1) 1
    else inner(i-1) + inner(i-2)
  })
  inner(n)
}

The running time is dramatically improved and we can compute much larger Fibonacci numbers much faster:

scala> measureCpuTime { fib(1000) }
res14: (BigInt, Double) = (<A number with 209 digits>,0.001016623)

This memoization is a key component in dynamic programming. Let’s study the call tree for fib(6) with memoization:

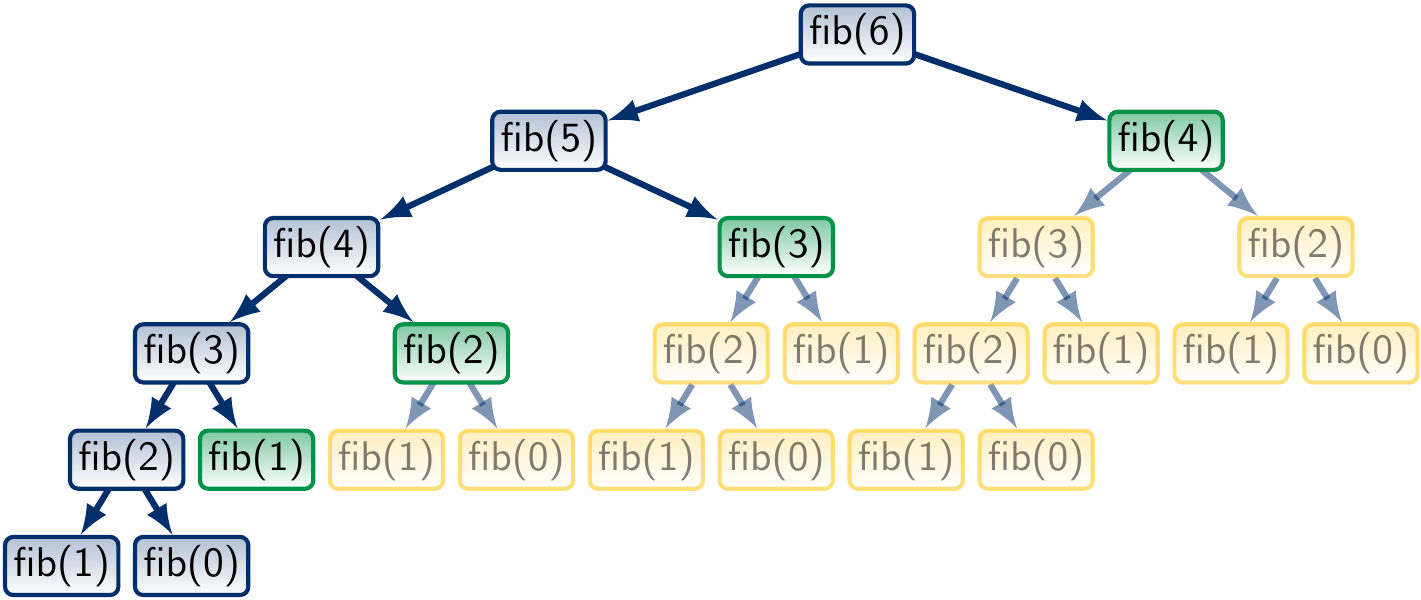
Here the green nodes are those whose value is found in the memoization map and whose subtrees, marked in yellow, are not traversed at all. We observe that a significant part of the call tree is not traversed at all.

What then is the time-complexity of this improved algorithm? It is the number of different function invocations times the amount of the time spent in each. Assuming constant-time addition and map lookup+update (as we have seen earlier, map lookup+update is actually $ \Oh{\log n} $ or $ \Oh{1} $ on average), the complexity is $$n \times \Oh{1} = \Oh{n}$$ No recurrences were need in computing this. If we want to be more precise and take into account the linear time of adding two $ \Theta(n) $ bit numbers, then the worst-case running time is $$T(n) = T(n-1)+\Theta(n)=\Theta(n^2)$$ The memory consumption of the algorithm $ \Theta(n^2) $ as well as the map stores $ n $ numbers with $ \Oh{n} $ bits each.

However, the recursive version is not tail recursive and thus can exhaust stack frame memory (recall the CS-A1120 Programming 2 course). We can also perform the same computations also iteratively bottom-up, starting from fib(0), saving the results in an array:

def fib(n: Int): BigInt = {
  require(n >= 0)
  val m = new Array[BigInt](n+1 max 2)
  m(0) = 0
  m(1) = 1
  for(i <- 2 to n) m(i) = m(i-2) + m(i-1)
  m(n)
}

scala> measureCpuTime { fib(1000) }
res17: (BigInt, Double) = (<A number with 209 digits>,7.05329E-4)

Now the lookup+update in arrays is quaranteed to work in constant time. However, the memory consumption is still $ \Theta(n^2) $.

In this simple example of Fibonacci numbers, we actually only have to remember the last two values and can thus reduce the amount of memory needed. Starting from $ F_0 $ and $ F_1 $, we simply iterate to $ F_n $:

def fib(n: Int): BigInt = {
  require(n >= 0)
  if(n == 0) return 0
  var fPrev = BigInt(0)
  var f = BigInt(1)
  for(i <- 1 until n) {
    val fNew = fPrev + f
    fPrev = f
    f = fNew
  }
  return f
}

scala> measureCpuTime { fib(1000) }
res48: (BigInt, Double) = (<A number with 209 digits>,6.0929E-4)

Now the memory consumption is reduced to $ \Theta(n) $.

The same can also be written in the functional style as follows:

def fib(n: Int): BigInt = {
  require(n >= 0)
  if(n == 0) 0
  else (1 until n).foldLeft[(BigInt,BigInt)](0,1)(
    {case ((fPrev,f),i) => (f, fPrev+f)})._2
}

Recap: typical steps in solving problems with dynamic programming¶

After the first example, we can now recap the main steps in applying dynamic programming to solving a computational problem.

Define the (optimal) solutions based on the (optimal) solutions to sub-problems. This leads to a recursive definition for the (optimal) solutions.

In the Fibonacci example, there was no optimality requirement, and the recursive definition was already given.
Check if the sub-solutions occur many times in the call trees.
If they do, apply memoization in the recursive version or build an iterative version using arrays to store sub-solutions.

In the Fibonacci example this was the case and we obtained substantial improvements in performance when compared to the plain recursive version.

Example II: Rod cutting¶

Let’s consider a second example where the recursive definition is not given but we’ve to figure out one. Study the following optimization problem:

Problem: The rod cutting problem

We are given a rod of length $ n $ and an array $ \Seq{\Price{1},…,\Price{n}} $ of prices, each $ \Price{i} $ telling the amount of money we get if we sell a rod piece of length $ i $. We can cut the rod in pieces and making cuts is free.

What is the best way to cut the rod so that we get the maximum profit?

Example

Suppose that we have a rod of length $ 4 $ and that the prices are

$ 2 $ credits for rod units of length $ 1 $,
$ 4 $ credits for rod units of length $ 2 $,
$ 7 $ credits for rod units of length $ 3 $, and
$ 8 $ credits for rod units of length $ 4 $.

The best way to cut our rod is to make one piece of length $ 1 $ and one of length $ 3 $. Selling them gives us $ 9 $ credits.

Recursive formulation¶

How do we define the optimal solutions recursively? That is, how to cut a rod of length $ n $ to get maximum profit? Denote the maximum profit by $ \Profit{n} $. Now it is quite easy to observe that $ \Profit{n} $ is the maximum of the following profits:

Cut away a piece of length $ 1 $ and then cut the remaining rod of length $ n-1 $ in the best way $ \Rightarrow $ the profit is $ \Price{1} + \Profit{n-1} $.
Cut away a piece of length $ 2 $ and then cut the remaining rod of length $ n-2 $ in the best way $ \Rightarrow $ the profit is $ \Price{2} + \Profit{n-2} $.
$ \vdots $
Cut away a piece of length $ n-1 $ and then cut the remaining rod of length $ 1 $ in the best way $ \Rightarrow $ the profit is $ \Price{n-1} + \Profit{1} $.
Make no cuts, the profit is $ \Price{n} $.

Therefore, we can formulate $ \Profit{n} $ as $$\Profit{n} = \max_{i = 1,…,n} (\Price{i} + \Profit{n-i})$$ with the base case $ \Profit{0} = 0 $ so that the last “no cuts” case is treated uniformly. Again, once we have the recursive formulation, implementation is straightforward. For istance, in Scala we can write the following recursive function:

def cut(n: Int, prices: Array[Int]) = {
  require(prices.length >= n+1)
  require(prices(0) == 0 && prices.forall(_ >= 0))
  def inner(k: Int): Long = {
    if(k == 0) 0
    else {
      var best: Long = -1
      for(i <- 1 to k)
	best = best max (prices(i) + inner(k - i))
      best
    }
  }
  inner(n)
}

The same in functional style:

def cut(n: Int, prices: Array[Int]) = {
  require(prices.length >= n+1)
  require(prices(0) == 0 && prices.forall(_ >= 0))
  def inner(k: Int): Long = {
    if(k == 0) 0
    else (1 to k).iterator.map(i => prices(i) + inner(k - i)).max
  }
  inner(n)
}

Question: why is iterator used in the code above?

The call tree when $ n = 4 $ looks like this:

What is the worst-case running time of the program? In a rod of length $ n $, there are $ n-1 $ places where we can make a cut. Therefore, there are $ 2^{n-1} $ ways to cut the rod. As the algorithm generates each of them, its worst-case running time is $ \Theta(2^n) $.

We could have “optimized” the program by always taking the cuts of length 1 first, then those of length 2 and so on in our recursive definition. In this case, the number of ways the rod can be cut is the same as the number of ways a natural number $ n $ can be partitioned and is called the partition function $ p(n) $. Again, $ p(n) $ grows faster than any polynomial in $ n $ and the resulting algorithm would not be very efficient.

Dynamic programming with memoization¶

As in our previous example of Fibonacci numbers, we can use memoization to avoid solving the same sub-problems multiple times:

def cut(n: Int, prices: Array[Int]) = {
  require(prices.length >= n+1)
  require(prices(0) == 0 && prices.forall(_ >= 0))
  val m = scala.collection.mutable.Map[Int, Long]() // ADDED
  def inner(k: Int): Long = m.getOrElseUpdate(k, {  // CHANGED
    if(k == 0) 0
    else {
      var best: Long = -1
      for(i <- 1 to k)
	best = best max (prices(i) + inner(k - i))
      best
    }
  })
  inner(n)
}

Now the call tree for $ n = 4 $ is

where the green function calls are found in the memoization map and yellow ones are never invoked. The worst-case running time is obtained with the recurrences $ T(0) = \Oh{1} $ and $ T(n) = \Theta(n) + T(n-1) $. Therefore, $ T(n) = \Theta(n^2) $. The term $ \Theta(n) $ above is due to the for-loop over $ n $ values for finding the maximum one.

Constructing the solution¶

In the rod cutting problem, we are not only interested in the optimal price value but the also in how it can be obtained, i.e., how the rod should be cut in order to get the maximum profit. To have this information, we can simply record, in each call inner(k), not only the best profit but also which cutting produced that. There could be many cuttings that produce the best profit but we record only one because the number of such cuttings can be very large. The idea as code

def cut(n: Int, prices: Array[Int]) = {
  require(prices.length >= n+1)
  require(prices(0) == 0 && prices.forall(_ >= 0))
  val m = collection.mutable.Map[Int, (Long, List[Int])]() // CHANGED
  def inner(k: Int): (Long, List[Int]) = m.getOrElseUpdate(k, {
    if(k == 0) (0, Nil)
    else {
      var best: Long = -1
      var bestCuts: List[Int] = null       // ADDED
      for(i <- 1 to k) {
	val (subValue, subCuts) = inner(k - i)
	if(subValue + prices(i) > best) {
	  best = subValue + prices(i)
	  bestCuts = i :: subCuts          // ADDED
	}
      }
      (best, bestCuts)  // CHANGED
    }
  })
  inner(n)
}

The time-complexity remains to be $ \Oh{n^2} $.

The same in the iterative style

def cut(n: Int, prices: Array[Int]) = {
  require(prices.length >= n+1)
  require(prices(0) == 0 && prices.forall(_ >= 0))
  val m = new Array[(Long, List[Int])](n+1)
  m(0) = (0, Nil) // The base case
  for(k <- 1 to n) {
    var best: Long = -1
    var bestCuts: List[Int] = null
    for(i <- 1 to k) {
      val (subValue, subCuts) = m(k - i)
      if(subValue + prices(i) > best) {
	best = subValue + prices(i)
	bestCuts = i :: subCuts
      }
    }
    m(k) = (best, bestCuts)
  }
  m(n)
}

The space-complexity is $ \Theta(n) $. Question: why does the storing of the best solutions not increase the space-complexity to $ \Theta(n^2) $?

To recap: when is dynamic programming applicable? In general, dynamic programming can be applied when

we can defined the (optimal) solutions by using smaller (optimal) sub-problem solutions, and
the sub-problems overlap, meaning that the same sub-problem can be used multiple times.

Example III: Longest common subsequence¶

Let’s repeat the same process one more time. Now consider two sequences of symbols, say $ \LCSA = \Seq{\LCSa1,…,\LCSa{n}} $ and $ \LCSB = \Seq{\LCSb1,…,\LCSb{m}} $. They could be DNA sequences, written texts etc. We are interested in finding out how similar the sequences are. There are many measures for “similarity” but here we consider the following definitions:

A common subsequence of $ \LCSA $ and $ \LCSB $ is a sequence $ \LCSO = \Seq{\LCSo{1},…,\LCSo{k}} $ whose elements appear in the same order in both $ \LCSA $ and in $ \LCSB $.
A longest common subsequence (LCS) is a common subsequence of maximal length.

The longer the longest common subsequence(s) are, the more similar the strings are considered to be. The longest common subsequence problem is thus:

Given two sequences, find one of their longest common subsequences.

Example

Consider the sequences $ \LCSA = \Seq{A,C,G,T,A,T} $ and $ \LCSB = \Seq{A,T,G,T,C,T} $. Their (unique) longest common subsequence is $ \Seq{A,G,T,T} $.

Note

Note the longest common subsequences are not necessarily unique. For instance, take the sequences $ \LCSA = \Seq{C,C,C,T,T,T} $ and $ \LCSB = \Seq{T,T,T,C,C,C} $. Their LCSs are $ \Seq{C,C,C} $ and $ \Seq{T,T,T} $

A simple approach to solve the length of an LCS of sequences (and to find one) would be to generate, in a longest-first order, all the subsequences of another sequence and check for each whether it is also a subsequence of the other. Of course, this would be very inefficient as there are exponentially many subsequences.

Recursive definition¶

Again, in order to use dynamic programming, we have to develop a recursive definition for building optimal solutions from optimal solutions to sub-problems. Let’s use the definitions $ \LCSAP{i} = \Seq{\LCSa1,…,\LCSa{i}} $ for $ 0 \le i \le n $ and $ \LCSBP{j} = \Seq{\LCSb1,…,\LCSb{i}} $ for $ 0 \le j \le m $ to the denote prefixes of $ \LCSA $ and $ \LCSB $. We obtain a recursive definition by studying the last symbols in the sequences $ \LCSAP{n} = \Seq{\LCSa1,…,\LCSa{n}} $ and $ \LCSBP{m} = \Seq{\LCSb1,…,\LCSb{m}} $:

If $ \LCSa{n} = \LCSb{m} $, then we obtain an LCS of $ \LCSAP{n} $ and $ \LCSBP{m} $ by taking an LCS of $ \LCSAP{n-1} $ and $ \LCSBP{m-1} $ and concatenating it with $ \LCSa{n} $
If $ \LCSa{n} \neq \LCSb{m} $ and an LCS $ \LCSO $ of $ \LCSAP{n} $ and $ \LCSBP{m} $ does not contain $ \LCSa{n} $ as its last symbol, then $ \LCSO $ is an LCS of $ \LCSAP{n-1} $ and $ \LCSBP{m} $
If $ \LCSa{n} \neq \LCSb{m} $, and an LCS $ \LCSO $ of $ \LCSAP{n} $ and $ \LCSBP{m} $ does not contain $ \LCSb{m} $ as its last symbol, then $ \LCSO $ is an LCS of $ \LCSAP{n} $ and $ \LCSBP{m-1} $.

Naturally, when $ n = 0 $ or $ m = 0 $, the LCS is the empty sequence with length $ 0 $. Question: The definition above allows us to find an optimal solution, not all of them; why is this?

Example

Let’s illustrate the cases in the definition.

If $ \LCSAP{6} = \Seq{A,C,G,T,A,T} $ and $ \LCSBP{5} = \Seq{A,G,C,C,T} $, then their LCSs are $ \Seq{A,C,T} $ and $ \Seq{A, G, T} $. Both are obtained from the two LCSs $ \Seq{A,C} $ and $ \Seq{A,G} $ of $ \LCSAP{5}=\Seq{A,C,G,T,A} $ and $ \LCSBP{4}=\Seq{A,G,C,C} $ by concatenating them with the last symbol $ T $.
If $ \LCSAP{5} = \Seq{A,G,C,A,C} $ and $ \LCSBP{6} = \Seq{A,C,G,T,A,T} $, then their LCSs are $ \Seq{A,C,A} $ and $ \Seq{A,G,A} $. Neither contain $ C $ as the last symbol and both are the LCS of $ \LCSAP{4} = \Seq{A,G,C,A} $ and $ \LCSBP{6} = \Seq{A,C,G,T,A,T} $.
The third case is symmetric to the second case.

Again, once we have a recursive definition, an implementation follows quite easily:

def lcs(a: String, b: String) = {
  def inner(n: Int, m: Int): String = {
    if(n < 0) ""
    else if(m < 0) ""
    else if(a(n) == b(m)) inner(n-1, m-1) + a(n)
    else Seq(inner(n-1, m), inner(n, m-1)).maxBy(_.length)
  }
  inner(a.length-1, b.length-1)
}

Note: string indexing starts from 0, not from 1 as in “maths” above.

Again, this simple implementation implementation has exponential running time in the worst case. But for some inputs, such as lcs("abcab","cab"), it is quite fast; why is this the case? Note also that concatenating a single character at the end of a string is not a constant-time operation; thus the naive version above is not a very optimal solution in this sense either.

The call tree for the sequences “abac” and “acab” is:

The call tree for the sequences “ccc” and “bbb” is quite large already:

Dynamic programming with memoization¶

By simply applying memoization with mutable maps, we get the following version that only computes the length of the longest common subsequence.

def lcs(a: String, b: String) = {
  val mem = collection.mutable.HashMap[(Int,Int), Int]() // ADDED
  def inner(n: Int, m: Int): Int = mem.getOrElseUpdate((n, m), { //CHANGED
    if(n < 0) 0
    else if(m < 0) 0
    else if(a(n) == b(m)) inner(n-1, m-1) + 1
    else Seq(inner(n-1, m), inner(n, m-1)).max
  })
  inner(a.length-1, b.length-1)
}

Justify the following claim:

The running time of the algorithm above is $ \Oh{n m} $, where $ n $ is the length of the string $ a $ and $ m $ that of $ b $.

We can add solution reconstruction as a separate phase. When it is called, the memoization map has been completely filled and we can use it instead of recomputing the values. Observe that we also construct the solution in reverse order by using a list (in which prepending an element is cheap) and then reverse the answer at the end.

def lcs(a: String, b: String) = {
  val mem = scala.collection.mutable.HashMap[(Int,Int), Int]()
  def inner(n: Int, m: Int): Int = mem.getOrElseUpdate((n, m), {
    if(n < 0) 0
    else if(m < 0) 0
    else if(a(n) == b(m)) inner(n-1, m-1)+1
    else Seq(inner(n-1, m), inner(n, m-1)).max
  })
  inner(a.length-1, b.length-1)
  def reconstruct(n: Int, m:Int): List[Char] = {
    if(n < 0) Nil
    else if(m < 0) Nil
    else if(a(n) == b(m)) a(n) :: reconstruct(n-1, m-1)
    else if(mem(n, m) == mem(n-1, m)) reconstruct(n-1, m)
    else reconstruct(n,m-1)
  }
  reconstruct(a.length-1, b.length-1).reverse.mkString("")
}

An iterative version with arrays¶

The main problem with recursive implementations, even when memoization is used, is that the recursion depth can be large and cause stack overflow errors in systems (such as Java VM) with a fixed amount of memory allocated for the call stack. For instance, if we apply the recursive Scala program above on two strings with thousands of characters having a long LCS, a stack overflow error will occur in a typically configured JVM setting. To avoid this, we can provide a non-recursive version that stores the length of the LCS of $ \LCSAP{i} $ and $ \LCSBP{j} $ in the entry table[i,j] of a two-dimensional array table, and works bottom up,

starting from the base cases when $ i = 0 $ or $ j = 0 $, and
computing the values of table[i-1,j], table[i,j-1], and table[i-1,j] before table[i,j].

The final result is then the the last entry table(n,m).

def lcs(x: String, y: String): String = {
  val (n, m) = (x.length, y.length)
  val table = Array.tabulate[Int](n+1,m+1)({case (i,j) => 0})
  for(i <- 1 to n; j <- 1 to m) {
    if(x(i-1) == y(j-1))
      table(i)(j) = table(i-1)(j-1) + 1
    else if(table(i-1)(j) >= table(i)(j-1))
      table(i)(j) = table(i-1)(j)
    else
      table(i)(j) = table(i)(j-1)
  }
  // Reconstruct a solution
  var i = n
  var j = m
  var solution: List[Char] = Nil
  while(i > 0 && j > 0) {
    if(x(i-1) == y(j-1)) {
      solution = x(i-1) :: solution
      i -= 1
      j -= 1
    }
    else if(table(i-1)(j) >= table(i)(j-1)) i -= 1
    else j -= 1
  }
  solution.mkString("")
}

The constructed table can be illustrated for the sequences $ \LCSA = \Seq{A,G,C,T,C,T} $ and $ \LCSB = \Seq{A,C,G,T,A,T} $ as below:

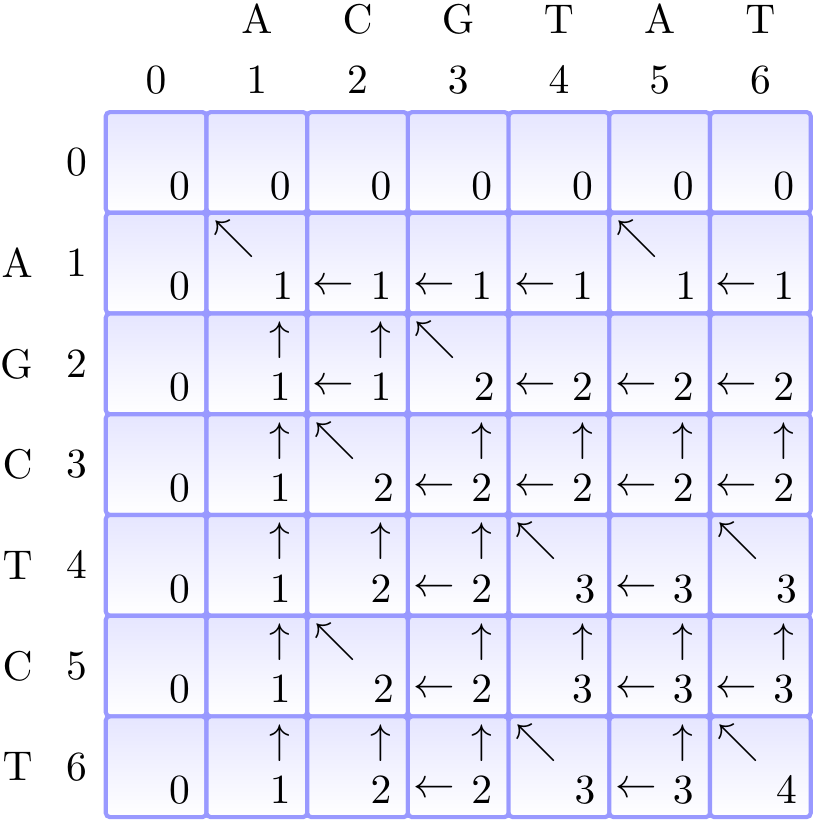
In the picture, the arrows describe the direction(s) which produce a solution in the recursive definition.