3.7. Implementing Recursion¶

WARNING! You should not read this section unless you are already comfortable with implementing recursive functions. One of the biggest hang-ups for students learning recursion is too much focus on the recursive "process". The right way to think about recursion is to just think about the return value that the recursive call gives back. Thinking about how that answer is computed just gets in the way of understanding. There are good reasons to understand how recursion is implemented, but helping you to write recursive functions is not one of them.

Perhaps the most common computer application that uses stacks is not even visible to its users. This is the implementation of subroutine calls in most programming language runtime environments. A subroutine call is normally implemented by pushing necessary information about the subroutine (including the return address, parameters, and local variables) onto a stack. This information is called an activation record. Further subroutine calls add to the stack. Each return from a subroutine pops the top activation record off the stack. As an example, here is a recursive implementation for the factorial function.

// Recursively compute and return n!
static long rfact(int n) {
  // fact(20) is the largest value that fits in a long
  if ((n < 0) || (n > 20)) return -1;
  if (n <= 1)  return 1;  // Base case: return base solution
  return n * rfact(n-1);   // Recursive call for n > 1
}

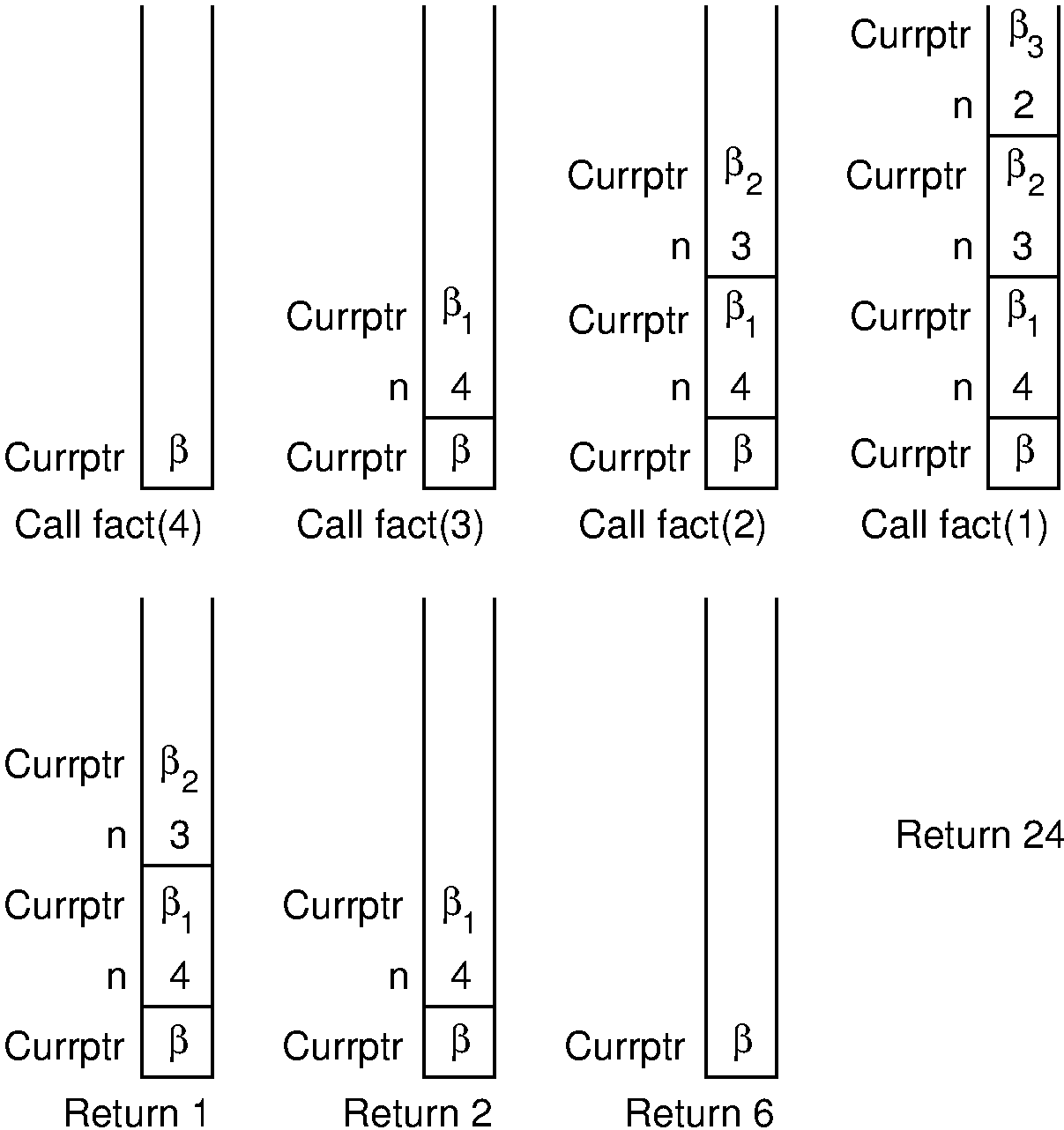
Here is an illustration for how the internal processing works.

\(\beta\) values indicate the address of the program instruction to return to after completing the current function call. On each recursive function call to fact, both the return address and the current value of n must be saved. Each return from fact pops the top activation record off the stack.

Consider what happens when we call fact with the value 4. We use \(\beta\) to indicate the address of the program instruction where the call to fact is made. Thus, the stack must first store the address \(\beta\), and the value 4 is passed to fact. Next, a recursive call to fact is made, this time with value 3. We will name the program address from which the call is made \(\beta_1\). The address \(\beta_1\), along with the current value for \(n\) (which is 4), is saved on the stack. Function fact is invoked with input parameter 3.

In similar manner, another recursive call is made with input parameter 2, requiring that the address from which the call is made (say \(\beta_2\)) and the current value for \(n\) (which is 3) are stored on the stack. A final recursive call with input parameter 1 is made, requiring that the stack store the calling address (say \(\beta_3\)) and current value (which is 2).

At this point, we have reached the base case for fact, and so the recursion begins to unwind. Each return from fact involves popping the stored value for \(n\) from the stack, along with the return address from the function call. The return value for fact is multiplied by the restored value for \(n\), and the result is returned.

Because an activation record must be created and placed onto the stack for each subroutine call, making subroutine calls is a relatively expensive operation. While recursion is often used to make implementation easy and clear, sometimes you might want to eliminate the overhead imposed by the recursive function calls. In some cases, such as the factorial function above, recursion can easily be replaced by iteration.

// Return n!
static long sfact(int n) {
  // fact(20) is the largest value that fits in a long
  if ((n < 0) || (n > 20)) return -1;
  // Make a stack just big enough
  Stack S = new AStack(n);
  while (n > 1) S.push(n--);
  long result = 1;
  while (S.length() > 0)
    result = result * (Integer)S.pop();
  return result;
}

An iterative form of the factorial function is both simpler and faster than the version shown in the example. But it is not always possible to replace recursion with iteration. Recursion, or some imitation of it, is necessary when implementing algorithms that require multiple branching such as in the Towers of Hanoi algorithm, or when traversing a binary tree. The Mergesort and Quicksort sorting algorithms also require recursion. Fortunately, it is always possible to imitate recursion with a stack. Let us now turn to a non-recursive version of the Towers of Hanoi function, which cannot be done iteratively.

// Compute the moves to solve a Tower of Hanoi puzzle.
// Function move does (or prints) the actual move of a disk
// from one pole to another.
// n: The number of disks
// start: The start pole
// goal: The goal pole
// temp: The other pole
static void TOHr(int n, Pole start, Pole goal, Pole temp) {
  if (n == 0) return;          // Base case
  TOHr(n-1, start, temp, goal); // Recursive call: n-1 rings
  move(start, goal);            // Move bottom disk to goal
  TOHr(n-1, temp, goal, start); // Recursive call: n-1 rings
}

// Compute the moves to solve a Tower of Hanoi puzzle.
// Function move does (or prints) the actual move of a disk
// from one pole to another.
// n: The number of disks
// start: The start pole
// goal: The goal pole
// temp: The other pole
static void TOH(int n, Pole start, Pole goal, Pole temp) {
  if (n == 0) return;          // Base case
  TOH(n-1, start, temp, goal); // Recursive call: n-1 rings
  move(start, goal);            // Move bottom disk to goal
  TOH(n-1, temp, goal, start); // Recursive call: n-1 rings
}

static class TOHobj {
  int op;
  int num;
  Pole start, goal, temp;

  // Recursive call operation
  TOHobj(int o, int n, Pole s, Pole g, Pole t)
  { op = o; num = n; start = s; goal = g; temp = t; }

  // MOVE operation
  TOHobj(int o, Pole s, Pole g)
  { op = o; start = s; goal = g; }
}

static void TOHs(int n, Pole start, Pole goal, Pole temp) {
  // Make a stack just big enough
  Stack S = new AStack(2*n+1);
  S.push(new TOHobj(TOH, n, start, goal, temp));
  while (S.length() > 0) {
    TOHobj it = (TOHobj)S.pop();   // Get next task
    if (it.op == MOVE) // Do a move
      move(it.start, it.goal);
    else if (it.num > 0) { // Imitate TOH recursive solution (in reverse)
      S.push(new TOHobj(TOH, it.num-1, it.temp, it.goal, it.start));
      S.push(new TOHobj(MOVE, it.start, it.goal));  // A move to do
      S.push(new TOHobj(TOH, it.num-1, it.start, it.temp, it.goal));
    }
  }
}

class TOHobj {
  int op;
  int num;
  Pole start, goal, temp;

  // Recursive call operation
  TOHobj(int o, int n, Pole s, Pole g, Pole t)
  { op = o; num = n; start = s; goal = g; temp = t; }

  // MOVE operation
  TOHobj(int o, Pole s, Pole g)
  { op = o; start = s; goal = g; }
}

void TOHs(int n, Pole start, Pole goal, Pole temp) {
  // Make a stack just big enough
  Stack S = new AStack(2*n+1);
  S.push(new TOHobj(TOH, n, start, goal, temp));
  while (S.length() > 0) {
    TOHobj it = (TOHobj)S.pop();   // Get next task
    if (it.op == MOVE) // Do a move
      move(it.start, it.goal);
    else if (it.num > 0) { // Imitate TOH recursive solution (in reverse)
      S.push(new TOHobj(TOH, it.num-1, it.temp, it.goal, it.start));
      S.push(new TOHobj(MOVE, it.start, it.goal));  // A move to do
      S.push(new TOHobj(TOH, it.num-1, it.start, it.temp, it.goal));
    }
  }
}

Recursive algorithms lend themselves to efficient implementation with a stack when the amount of information needed to describe a sub-problem is small. For example, Quicksort can effectively use a stack to replace its recursion since only bounds information for the subarray to be processed needs to be saved.