Moniulotteiset listat
Tarkastellaan ongelmaa, jossa halutaan esittää matriiseja Python-ohjelmassa. Matriisi koostuu riveistä ja sarakkeista, esimerkiksi
Tässä matriisissa on siis neljä riviä ja kolme saraketta. Matriiseja tarvitaan hyvin yleisesti esimerkiksi erilaisissa tekniikan alan laskutoimituksissa.
Miten sitten matriisia voidaan käsitellä Python-ohjelmassa? On toki
mahdollista esittää kaikki matriisin alkiot yhtenä listana eli
esimerkkimatriisi listana
[1, 5, 8, 3, 19, 25, 11, 21, 70, 31, 4, 41]. Tässä listassa ei
kuitenkaan näy mitenkään matriisin rakenne eli sen jako riveihin ja
sarakkeisiin. Matriisien laskutoimituksissa on tärkeä merkitys sillä,
millä rivillä ja missä sarakkeessa kukin alkio on. Vaikka tämän
pystyykin laskemaan alkion indeksistä, olisi kätevämpää, jos indeksit
kertoisivat suoraan alkion rivin ja sarakkeen matriisissa.
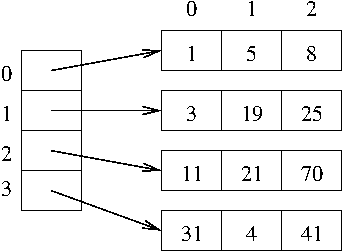
Parempi vaihtoehto on käyttää kaksiulotteista listaa. Siinä listan
jokaista riviä vastaa yksi listan alkio. Tämä alkio ei kuitenkaan ole
yksittäinen luku, vaan toinen lista, jonka alkioina on riville kuuluvat
luvut. Esimerkkimatriisi esitettäisiin listana
[[1, 5, 8], [3, 19, 25], [11, 21, 70], [31, 4, 41]]. Rakenteen voi
ajatella näyttävän suunnilleen alla olevan kuvan mukaiselta (kuvaan on
merkitty myös listojen indeksejä niiden seuraamisen helpottamiseksi):
Jos ohjelmassa on suoritettu käsky
matriisi = [[1, 5, 8], [3, 19, 25], [11, 21, 70], [31, 4, 41]]
viittaa nyt matriisi koko esitettyyn kaksiulotteiseen listaan:
Sen sijaan matriisi[1] tarkoittaa listan toista alkiota, siis
toisena alkiona olevaa pikkulistaa.
Merkinnässä matriisi[1][2] ensimmäisten hakasulkujen sisällä oleva
indeksi tarkoittaa indeksiä varsinaisessa (ulommassa) listassa, toisten
hakasulkujen sisällä oleva indeksi taas tarkoittaa indeksiä ulomman
listan alkiona olevassa pikkulistassa:
Alla on esitetty esimerkkejä eri merkintöjen tarkoituksesta:
>>> print(matriisi)
[[1, 5, 8], [3, 19, 25], [11, 21, 70], [31, 4, 41]]
>>> print(matriisi[3])
[31, 4, 41]
>>> print(matriisi[2])
[11, 21, 70]
>>> print(matriisi[2][1])
21
Seuraava esimerkkiohjelma lukee käyttäjältä kaksi matriisia ja laskee
niiden summan. Ohjelmassa on omat funktionsa yhden matriisin lukemiseen,
kahden matriisin summamatriisin laskemiseen (summa lasketaan laskemalla
aina yhteenlaskettavien matriisien samassa paikassa olevat alkiot
yhteen) ja matriisin tulostamiseen riveittäin. Huomaa, että
pääohjelmassa pidetään huolta siitä, että matriisien koko on järkevä ja
että yhteenlaskettavat matriisit ovat samankokoisia. Jos tästä ei
huolehdittaisi pääohjelmassa, pitäisi esimerkiksi funktioon
laske_summa lisätä tarkistus yhteenlaskettavien matriisien koosta.
Matriisien käsittelyssä käytetään usein kahta sisäkkäistä toistokäskyä, joista ulompi käy läpi kaikki matriisin rivit ja sisempi yhden rivin kaikki sarakkeet.
Matriisien tulostuksessa kukin tulostusrivi kootaan merkkijonoista, jotka on saatu käyttämällä rivin jokaiseen alkioon vuorollaan merkkijonojen muotoilua.
# Funktio lukee kayttajalta matriisin alkiot. Matriisin
# rivien ja sarakkeiden maara annetaan parametreina.
# Funktio luo matriisia varten kaksiulotteisen listan,
# tallentaa luetut luvut siihen ja palauttaa alkiot
# sisaltavan listan.
def lue_matriisi(rivilkm, sarakelkm):
matriisi = []
print("Anna matriisin alkiot riveittain,")
print(rivilkm, "rivia ja", sarakelkm, "saraketta.")
for i in range(rivilkm):
rivi = [0.0] * sarakelkm
for j in range(sarakelkm):
rivi[j] = float(input())
matriisi.append(rivi)
return matriisi
# Funktio saa parametrina kaksi matriisia, jotka on tallennettu
# kaksiulotteisiin listoihin. Funktio laskee naiden matriisien
# summamatriisin ja palauttaa sita vastaavan kaksiulotteisen listan.
def laske_summa(mat1, mat2):
summamat = []
rivimaara = len(mat1) # ulomman listan alkioiden maara
sarakemaara = len(mat1[0]) # pikkulistan alkioiden maara
for i in range(rivimaara):
summarivi = [0.0] * sarakemaara
for j in range(sarakemaara):
summarivi[j] = mat1[i][j] + mat2[i][j]
summamat.append(summarivi)
return summamat
# Funktio saa parametrina matriisia esittavan kaksiulotteisen
# listan. Se tulostaa matriisin alkiot riveittain.
def tulosta_matriisi(matri):
rivit = len(matri)
sarakkeet = len(matri[0])
for i in range(rivit):
tulosrivi = ""
for j in range(sarakkeet):
tulosrivi += f"{matri[i][j]:8.2f}"
print(tulosrivi)
def main():
print("Ohjelma laskee kahden matriisin summan.")
riveja = int(input("Rivien lukumaara: "))
sarakkeita = int(input("Sarakkeiden lukumaara: "))
if riveja <= 0 or sarakkeita <= 0:
print("Liian vahan riveja tai sarakkeita.")
else:
matriisi1 = lue_matriisi(riveja, sarakkeita)
matriisi2 = lue_matriisi(riveja, sarakkeita)
summa = laske_summa(matriisi1, matriisi2)
print("Matriisin")
tulosta_matriisi(matriisi1)
print("ja matriisin")
tulosta_matriisi(matriisi2)
print("summa on")
tulosta_matriisi(summa)
main()
Sisemmät listat ovat ihan tavallisia listoja, joiden loppuun voidaan lisätä
uusia alkioita append-metodilla samoin kuin yksiulotteisiin listoihin.
Alla on tästä esimerkki, jossa on käyty läpi kaksiulotteisen listan sisempiä
listoja indeksin avulla ja lisätty jokaisen loppuun kokonaisluku 5.
isolista = [[1, 2], [3, 4]]
for i in range(len(isolista)):
isolista[i].append(5)
print(isolista)
Vaihtoehtoisesti voidaan käyttää muuttujaa viittaamaan kuhunkin sisempään listaan, kuten alla on tehty:
isolista = [[1, 2], [3, 4]]
for i in range(len(isolista)):
pikkulista = isolista[i]
pikkulista.append(5)
print(isolista)
Jos sisemmän listan indeksiä ei tarvita muuten, voidaan sisemmät listat käydä myös läpi for-käskyssä muuttujan avulla seuraavasti:
isolista = [[1, 2], [3, 4]]
for pikkulista in isolista:
pikkulista.append(5)
print(isolista)
Kaikki nämä kolme esimerkkiohjelmaa tulostavat täsmälleen saman rivin eli listan, jossa jokaisen sisemmän listan loppuun on lisätty luku 5:
[1, 2, 5], [3, 4, 5]]
Varsin yleinen virhe kaksiulotteisten listojen kanssa on se, että ei luoda omaa listaa jokaista sisempää listaa varten (vaikka tämä olisi tarkoitus), vaan oikeasti ulommassa listassa esiintyy sama alilista useampaan kertaan. Seuraava esimerkki havainnollistaa, mistä tässä on kysymys:
def main():
isolista = []
pikkulista = [0] * 5
for i in range(3):
isolista.append(pikkulista)
print("Lista aluksi:", isolista)
isolista[2][1] = 55
print("Lista muutoksen jalkeen:", isolista)
main()
Kun ohjelma suoritetaan, näyttää sen tulostus seuraavalta:
Lista aluksi: [[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]]
Lista muutoksen jalkeen: [[0, 55, 0, 0, 0], [0, 55, 0, 0, 0], [0, 55, 0, 0, 0]]
Huomataan, että vaikka sijoituskäsky isolista[2][1] = 55 näytti muuttavan vain
yhden alkion arvoa, niin yhteensä kolme nollaa oli muuttunut arvoksi 55. Tämä
johtuu siitä, että ulomman listan alkoina ei olekaan kolme toisistaan
riippumatonta sisempää listaa, vaan ihan sama sisempi lista kolmeen kertaan.
Kun tämän sisemmän listan yhden alkion arvoa muutetaan, näkyy se koko listan
tulostuksessa kolmeen kertaan. Sisempi lista on sama, koska se on luotu
yhden kerran ennen for-käskyn alkua. Toistokäskyn sisällä oleva append-käsky
lisää ulomman listan loppuun aina tämän saman listan. Tilanteesta, jossa
samaan listaan tai muuhun käsiteltävään asiaan on Python-ohjelmassa
viitattu useampaan eri kertaan, on kerrottu tarkemmin tämän kierroksen
luvussa Arvot ja viittaukset.
Jos halutaan, että ulompi lista sisältää aidosti eri listoja, pitää luoda uusi sisempi lista erikseen joka kerta, kun se lisätään ulompaan listaan. Näin on tehty alla olevassa ohjelmassa. Sen olennainen ero edelliseen ohjelmaan on siinä, että sisempi lista luodaan nyt toistokäskyn sisällä, jolloin oikeasti luodaan niin monta uutta listaa kuin mitä ulompaan listaan lisätään:
def main():
isolista = []
for i in range(3):
pikkulista = [0] * 5
isolista.append(pikkulista)
print("Lista aluksi:", isolista)
isolista[2][1] = 55
print("Lista muutoksen jalkeen:", isolista)
main()
Kun tämä ohjelma suoritetaan, näyttää tulostus seuraavalta:
Lista aluksi: [[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]]
Lista muutoksen jalkeen: [[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 55, 0, 0, 0]]
Viimeisenä esimerkkinä kaksiulotteisista listoista tässä luvussa esitetään yksinkertaistettu alku ohjelmalle, jota voisi käyttää jätkänshakki- (ristinolla) pelin tekemiseen. Ohjelmassa ei ole vielä varsinaista peliä eikä esimerkiksi sen tarkistusta, onko jompikumpi pelaajista jo saanut ruudukkoon tarpeeksi pitkän suoran. Tässä ohjelmassa ainoastaan luodaan neliön muotoinen ruudukko, jossa on aluksi pelkkiä _-merkkejä, jotka kuvaavat tyhjiä paikkoja. Tämän jälkeen pelaajat asettavat ruudukkoon vuorotellen X- ja O-merkkejä. Kummallakin pelaajalla on neljä vuoroa eli ohjelma ei mitenkään tarkista sitä, onko peli jo päättynyt. Lisäksi vuoro siirtyy toiselle pelaajalle siinäkin tapauksessa, että pelaaja yritti sijoittaa merkin ruutuun, joka ei ole tyhjä tai on pelialueen ulkopuolella. Oikeassa pelissä pelaajalta kysyttäisiin tällöin uutta merkin paikkaa, mutta tässä esimerkissä pääohjelma on haluttu pitää mahdollisimman yksinkertaisena.
# Funktio luo kaksiulotteisen listan, jossa seka ulomman etta sisemman
# listan alkioiden maara on parametrina annettu koko. Sisempien
# listojen jokaisella paikalla on merkki _ kuvaamassa tyhjaa ruutua.
# Funktio palauttaa luodun listan.
def alusta_ruudukko(koko):
ruudukko = []
for i in range(koko):
rivi = ['_'] * koko
ruudukko.append(rivi)
return ruudukko
# Funktio saa parametrina peliruudukkoa kuvaavan kaksiulotteisen listan,
# listan joka sisaltaa halutun ruudun x- ja y-koordinaatit seka
# haluttuun ruutuun sijoitettavan merkin. Vasemman ylakulman koordinaatit
# ovat [1, 1].
# Jos ruutu on ruudukon alueella ja tyhja (sisaltaa merkin _), funktio lisaa
# merkin tahan ruutuun ja palauttaa arvon True. Jos ruutu on jo varattu
# tai pelialueen ulkopuolella, merkkia ei lisata ja funktio palauttaa arvon False.
def lisaa_merkki(peliruudukko, ruutu, merkki):
x_koordinaatti = ruutu[0] - 1
y_koordinaatti = ruutu[1] - 1
if 0 <= x_koordinaatti < len(peliruudukko) and \
0 <= y_koordinaatti < len(peliruudukko) and \
peliruudukko[y_koordinaatti][x_koordinaatti] == '_':
peliruudukko[y_koordinaatti][x_koordinaatti] = merkki
return True
else:
return False
# Funktio tulostaa peliruudukon (parametrina annetun kaksiulotteisen listan).
# Kukin sisempi lista (ruudukon rivi) tulostetaan omalle rivilleen.
# Peliruudukon merkkien ymparille lisataan lainausmerkit, jotta tulostuksessa
# ruudukon muoto olisi lahempana neliota.
def tulosta_ruudukko(pelialue):
for i in range(len(pelialue)):
for j in range(len(pelialue)):
print(' ' + pelialue[i][j] + ' ', end='')
print()
def main():
VUOROT = 4
pelilauta = alusta_ruudukko(6)
vuorossa = 'X'
for i in range(2 * VUOROT):
print(f"Anna pelaajan {vuorossa} seuraavan merkin koordinaatit")
x = int(input("x-koodinaatti: "))
y = int(input("y-koordinaatti: "))
lisaa_merkki(pelilauta, [x, y], vuorossa)
if vuorossa == 'X':
vuorossa = 'O'
else:
vuorossa = 'X'
tulosta_ruudukko(pelilauta)
main()
Alla on esimerkki tämän ohjelman suorituksesta. Peli jää tosiaan kesken, koska pääohjelma antaa pelaajille vakiomäärän vuoroja eikä se mitenkään tarkista, onko peli jo päättynyt. Ohjelmn päättyessä jälkimmäisellä pelaajalla on ruudukossa yksi merkki vähemmän kuin ensimmäisellä, koska jälkimmäinen pelaaja yritti yhdellä vuorolla sijoittaa merkkinsä ruudukossa jo olevan merkin päälle.
Lukija voi halutessaan täydentää ohjelman kokonaiseksi peliksi.
Anna pelaajan X seuraavan merkin koordinaatit
x-koodinaatti: 3
y-koordinaatti: 5
_ _ _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _
_ _ X _ _ _
_ _ _ _ _ _
Anna pelaajan O seuraavan merkin koordinaatit
x-koodinaatti: 2
y-koordinaatti: 1
_ O _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _
_ _ X _ _ _
_ _ _ _ _ _
Anna pelaajan X seuraavan merkin koordinaatit
x-koodinaatti: 3
y-koordinaatti: 4
_ O _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _
_ _ X _ _ _
_ _ X _ _ _
_ _ _ _ _ _
Anna pelaajan O seuraavan merkin koordinaatit
x-koodinaatti: 4
y-koordinaatti: 4
_ O _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _
_ _ X O _ _
_ _ X _ _ _
_ _ _ _ _ _
Anna pelaajan X seuraavan merkin koordinaatit
x-koodinaatti: 3
y-koordinaatti: 3
_ O _ _ _ _
_ _ _ _ _ _
_ _ X _ _ _
_ _ X O _ _
_ _ X _ _ _
_ _ _ _ _ _
Anna pelaajan O seuraavan merkin koordinaatit
x-koodinaatti: 3
y-koordinaatti: 5
_ O _ _ _ _
_ _ _ _ _ _
_ _ X _ _ _
_ _ X O _ _
_ _ X _ _ _
_ _ _ _ _ _
Anna pelaajan X seuraavan merkin koordinaatit
x-koodinaatti: 3
y-koordinaatti: 2
_ O _ _ _ _
_ _ X _ _ _
_ _ X _ _ _
_ _ X O _ _
_ _ X _ _ _
_ _ _ _ _ _
Anna pelaajan O seuraavan merkin koordinaatit
x-koodinaatti: 3
y-koordinaatti: 1
_ O O _ _ _
_ _ X _ _ _
_ _ X _ _ _
_ _ X O _ _
_ _ X _ _ _
_ _ _ _ _ _