Extra: Cryptographic hash functions

This section is not included in the examination requirements of the course.

Cryptographic hash functions are hash functions that produce “message digests” (hash values) for the given “messages” (text, file, or any other bit sequence). They should have some special properties:

it should be (relatively) efficient to compute digests but
it should be computationally extremely difficult to produce another message that has the same digest, and
a small change in the message should produce a digest that seems uncorrelated to the digest of the original.

Example

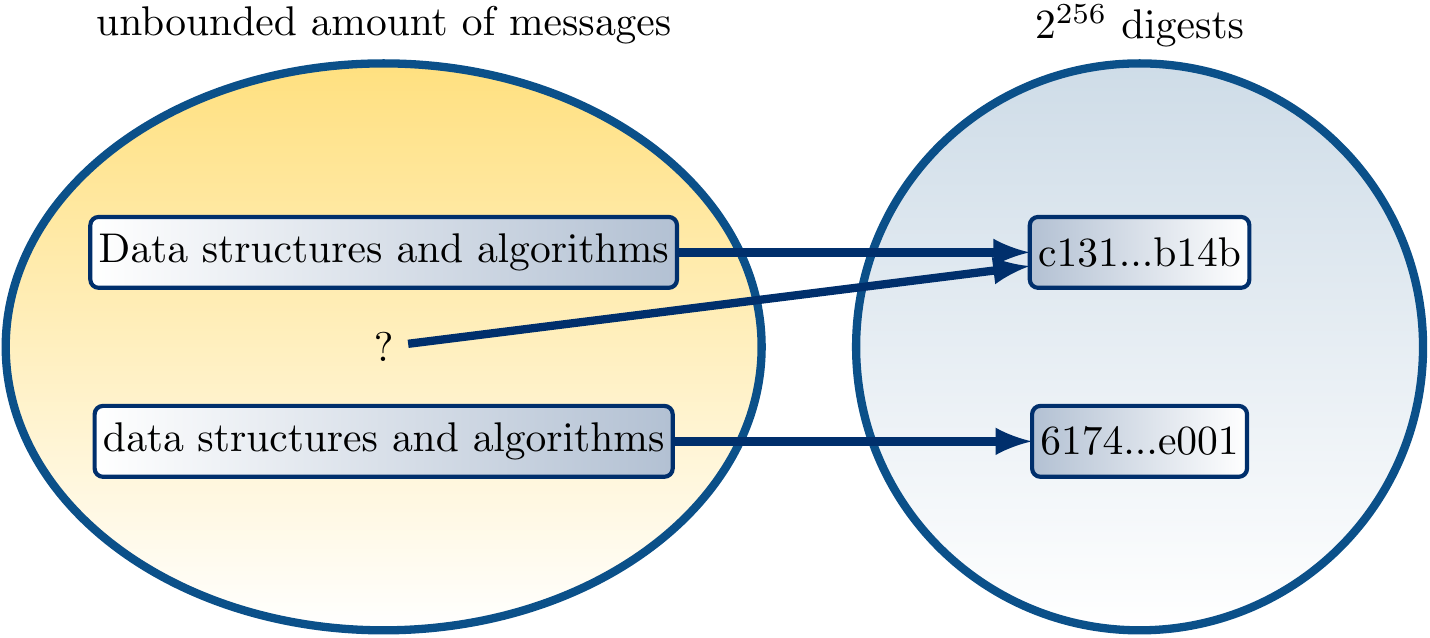
The figure below shows two slightly modified strings and their 256-bit long SHA-256 digests in hexadecimal. Observe the a very small change in the message results in a very different digest. The message “?” illustrates that is (currently, at least) infeasible to produce another string that has the same digest as “Data structures and algorithms”.

Applications of cryptographic hash functions include the following:

To check that the downloaded file (from a potentially unreliable source such as P2P or content delivery network) is uncorrupted, compare the computed digest to one downloaded from a reliable source.

File and data identifiers in Git and elsewhere are computed by hashing them.

mycomputer$ git log
commit 6cb618e84b004a9d968efeedf8b5b453e27879c3
Author: Tommi Junttila <Tommi.Junttila@aalto.fi>
Date:   Fri Sep 18 11:33:26 2020 +0300

    Heaps improved

Passwords are not stored in plain text in computers. Instead, they are first “salted” with a random number and then hashed.
```
tommi:$4$Tn6KDIg4$pzeSv2cT/YCiQ3W2w0M5DOg60JAlBUGk
AqsojZ9w2LEwM6rjKjt5pSfVHkXGibCgx04yAQ/MK/uZGxs2gF
e22Q:17003:0:99999:7:::
```
In digital signatures, hashing is can be used to “compress” the message to be signed. Thus the other, computationally more demanding phases can work on a smaller amount of data.
In Bitcoin and elsewhere, partial reverse hash computations are used to produce “proof of work”.

As an example of a cryptographic hash function, the SHA-256 function computes 256 bits long digests. This means that there are $2^{256}$ possible digests. To get an idea how large this number is, note that $2^{256} \approx 1.16 \times 10^{77}$. According to some estimates, the whole observable universe contains between $10^{78}$ to $10^{82}$ atoms. If one would like to produce two messages that have the same digest by taking hashing random messages, then one should take $4.0 \times 10^{38}$ random messages to succeed with probability $0.5$. That sounds very nice, but note that cryptographic hash functions are subject to constant mathematical attack attempts. For instance, the predecessor of SHA-256, named SHA-1, was broken in 2017.

Example: Computing SHA-256 digests of strings in Scala

The Java standard library has an implementation of the SHA-256 function. It can be called from Scala as shown below.

scala> import java.security.MessageDigest
scala> def sha256(s: String) = MessageDigest.getInstance("SHA-256").digest(s.getBytes("UTF-8")).map("%02x".format(_)).mkString

scala> sha256("Data structures and algorithms")
res0: String = c131186357151498f8757c045e13d7b1f980343218e45a39bb37ccd0e295b14b

scala> sha256("data structures and algorithms")
res1: String = 6174490c5ffbd68d0749391188e2a6b73a046f8d98c00028bf1aeb1db1bce001