How to prove a new problem NP-complete?

Suppose that we are given a new problem \(C\) that we suspect to be \(\NP\)-complete. To prove that \(C\) is indeed \(\NP\)-complete, we have to

show that it is in \(\NP\),
take any existing \(\NP\)-complete problem \(A\), and
reduce \(A\) to the new problem \(C\).

Because polynomial-time reductions compose, the existence of the reduction \(S\) from the \(\NP\)-complete problem \(A\) to \(C\) actually shows that \(C\) is also \(\NP\)-complete: for any problem \(B\) in \(\NP\), we can now build a reduction from \(B\) to \(C\) by

first reducing the instance \(x\) of \(B\) to an instance \(R(x)\) of \(A\) (such a reduction \(R\) exists because \(A\) is \(\NP\)-complete), and
then reducing the instance \(R(x)\) to the instance \(S(R(x))\) of \(C\). The instance \(x\) is a “yes” instance of \(B\) if and only if \(S(R(x))\) is a “yes” instance of \(C\).

As a consequence, if the new problem \(C\) can be solved in polynomial time, then so can \(A\) and all the other problems in \(\NP\).

Usually, but not always, the first step of showing that the new problem is in \(\NP\), meaning that it has polynomial-sized certificates that can be verified in polynomial time, is easy. The real difficulty is to choose the \(\NP\)-complete problem \(A\) carefully so that defining the polynomial-time reduction from \(A\) to \(C\) is as easy as possible.

Example: Independent set

Consider the following problem:

Definition: \(\Prob{recruiting strangers}\)

INSTANCE: A social network of students and a positive integer \(K\), where a social network consist of (i) a finite set of students and (ii) a symmetric, binary “knows” relation over the students.

QUESTION: is it possible to recruit \(K\) students so that none of these students knows each other?

Example

Consider the instance with the network drawn below and \(K=3\). Is it possible to find 3 students so that none of them knows any of the others?

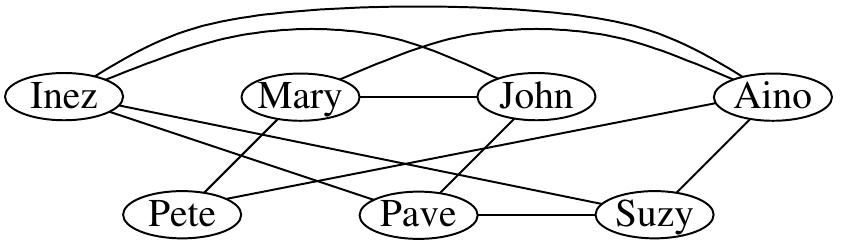
This instance is indeed a “yes” instance, the green vertices below show a solution. Is the solution the only one or are there others?

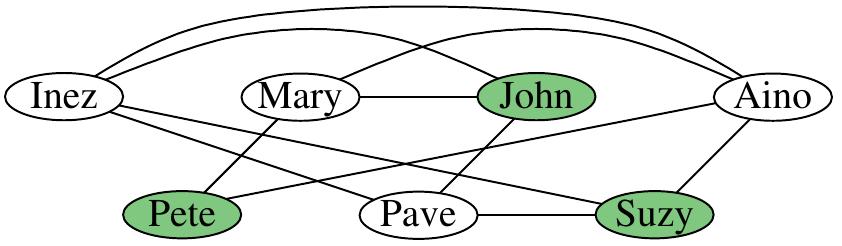
This problem is in fact equivalent to a well-known graph problem called \(\ISET\):

Definition: \(\ISET\)

INSTANCE: An undirected graph \(G = (V,E)\) and an integer \(K\).

QUESTION: Is there an independent set \(I \subseteq V\), with \(\Card{I} = K\)? (A set \(I \subseteq V\) is an independent set if for all distinct \(u,w \in I\), \(\Set{u,w} \notin E\).)

The \(\ISET\) problem is one of the classic \(\NP\)-complete problems, let’s now show this fact with a semi-formal proof.

Theorem

\(\ISET\) is \(\NP\)-complete.

Proof: sketch

We reduce from the \(\SATT\) problem. We are given a 3-CNF formula \(\phi = C_1 \land ... \land C_m\) with \(m\) clauses, each \(C_i = (l_{i,1} \lor l_{i,2} \lor l_{i,3})\) having exactly three literals over distinct variables. We form the corresponding \(\ISET\) instance by letting \(K = m\) and building the graph \(G\) as follows.

For each clause \(C_i = (l_{i,1} \lor l_{i,2} \lor l_{i,3})\), the graph contains the vertices \(v_{i,1}\), \(v_{i,2}\), and \(v_{i,3}\). Intuitively, the vertex \(v_{i,p}\) corresponds to the literal \(l_{i,p}\) (either \(x\) or \(\neg x\) for some variable \(x\)) of the clause.
There is an edge between two vertices \(v_{i,p}\) and \(v_{j,q}\) if and only if either
- \(i = j\), meaning that the vertices correspond literals in the same clause, or
- \(l_{i,p} = x\) and \(l_{j,q} = \neg x\) (or vice versa) for some variable \(x\).

The first edge condition above guarantees that only one of the vertices corresponding to literals in the same clause can be selected in an independent set. The second one guarantees that if we select a vertex corresponding to a literal \(x\) in the independent set, then we cannot include any vertex corresponding to the literal \(\neg x\) (and vice versa).

Suppose that \(\phi\) is satisfied by a truth assignment \(\TA\). Then we can form the independent set \(I\) of size \(K = m\) as follows. For each clause \(C_i = (l_{i,1} \lor l_{i,2} \lor l_{i,3})\), \(\TA(l_{i,p}) = \True\) for at least one literal in it because \(\TA\) satisfied \(\phi\): select one of such literals and include the corresponding vertex in the graph in \(I\). The set \(I\) has \(m\) elements as is an independent set because we selected only one vertex in each “clause triangle” and never selected a literal and its negation.

On the other hand, suppose that \(I\) is an independent set of size \(K = m\). In this case, we can form a truth assignment \(\TA\) that satisfies \(\phi\) as follows. For each clause \(C_i = (l_{i,1} \lor l_{i,2} \lor l_{i,3})\), the independent set must contain exactly one of the vertices \(v_{i,1}\), \(v_{i,2}\), and \(v_{i,3}\), otherwise it could not be of size \(m\) or an independent set. Select the literal \(l\) corresponding to that vertex and let \(\TA(x) = \True\) if \(l = x\) and \(\TA(x) = \False\) if \(l = \neg x\) for a variable \(x\). After done for all the clauses, the truth assignment satisfies each of the clauses. It may still have some variables that do not have a value, let them have the value \(\False\).

As a consequence:

If \(\phi\) is satisfiable, then \(G\) has an independent set of size \(K\).
If \(G\) has an independent set of size \(K\), then \(\phi\) is satisfiable.
\(\phi\) is satisfiable if and only if \(G\) has an independent set of size \(K\).

Because of the above theorem, If we could solve \(\ISET\) in polynomial time, then we could solve \(\SAT\) and all other problems in \(\NP\) in polynomial time as well.

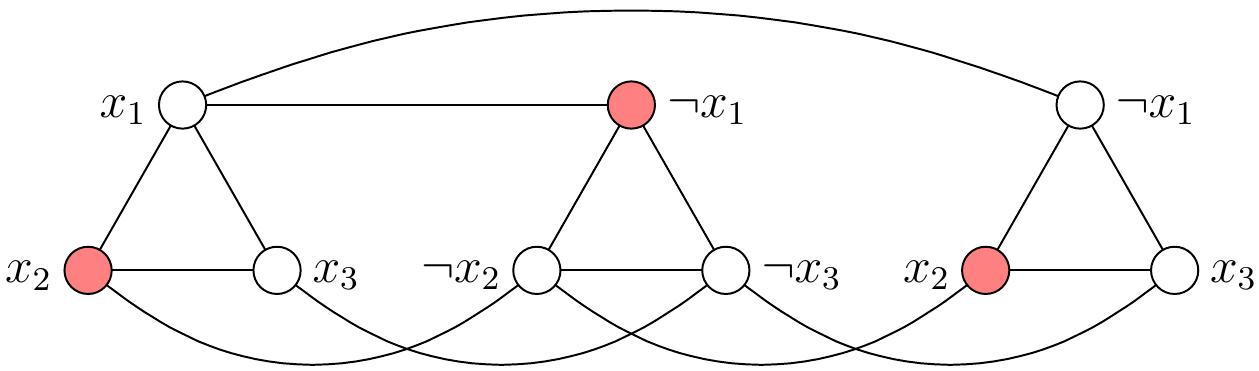
Example: Reduction from \(\SATT\) to \(\ISET\)

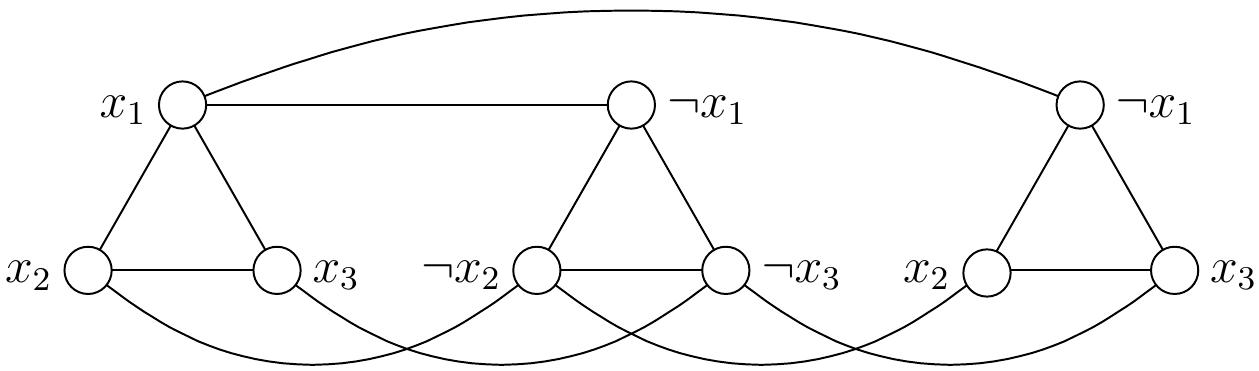
Consider the 3-CNF formula \(\phi = (x_1 \lor x_2 \lor x_3)\land (\neg x_1 \lor \neg x_2 \lor \neg x_3) \land (\neg x_1 \lor x_2 \lor x_3)\).

The corresponding \(\ISET\) problem instance consists of the graph \(G\) below and the independent set size requirement \(K=3\):

The formula \(\phi\) is satisfiable. For any satisfying truth assignment, such as \(\TA = \{x_1 \mapsto \True,x_2 \mapsto \True,x_3 \mapsto \False\}\), we can get an independent set of size 3 by taking, for each “clause triangle”, one of the vertices that correspond to a literal that evaluates to true in that clause under the assignment. For instance, the red vertices in the graph below show one possibility for the assignment \(\TA\) above.

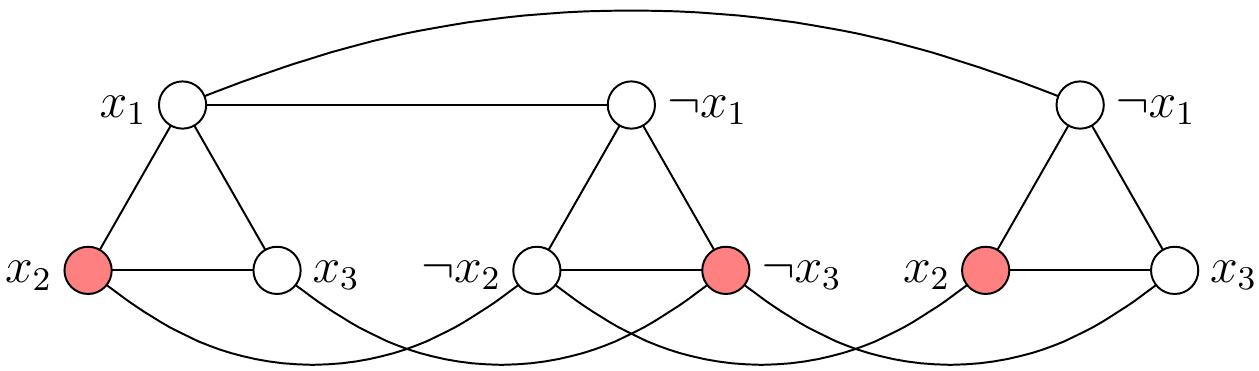
Conversely, from any independent set of size 3 in the graph, we obtain a truth assignment \(\TA\) that satisfies the formula \(\phi\) by letting \(\TA(x) = \True\) if a vertex with label \(x\) is in the independent set, and \(\TA(x) = \False\) otherwise. For instance, consider the independent set shown below in red. From this, we obtain the truth assignment \(\TA = \{x_1 \mapsto \False, x_2 \mapsto \True, x_3 \mapsto \False\}\) that satisfies \(\phi\).

Example: subset-sum

The \(\SUBSETSUM\) problem is in \(\NP\) as we can easily check whether a set of numbers (i) is a subset of the given set of numbers, and (ii) adds to the target value \(t\). We can show that \(\SUBSETSUM\) is NP-complete by reducing \(\SATT\) to it. Suppose that we are given a CNF formula \(\phi = C_1 \land ... \land C_m\), where each clause \(C_i\) contains 3 literals over distinct variables. Let the variables occurring in \(\phi\) be \(x_1,...,x_n\). We now build (in polynomial time) an instance \(\Tuple{S_{\phi},t_{\phi}}\) of \(\SUBSETSUM\) so that

\(\phi\) is satisfiable if and only if \(S_{\phi}\) has a subset summing to \(t_{\phi}\).

Therefore, if we could solve \(\SUBSETSUM\) in polynomial time, then we could solve \(\SATT\) in polynomial time as well. The polynomial-time reduction works as follows.

The numbers in \(S_{\phi}\) and \(t_{\phi}\) are base-10 numbers consisting of \(n+m\) digits \(\hat x_1 ... \hat x_n \hat C_1 ... \hat C_m\).
For each variable \(x_i\), the set \(S_{\phi}\) includes two numbers:
- \(v_i\) with the digit \(\hat x_i = 1\) and the digits \(\hat C_j = 1\) for each clause \(C_j\) containing the literal \(x_i\); the other digits are 0.
- \(v'_i\) with the digit \(\hat x_i = 1\) and the digits \(\hat C_j = 1\) for each clause \(C_j\) containing the literal \(\neg x_i\); the other digits are 0.
For each clause \(C_j\), the set \(S_{\phi}\) has two numbers:
- \(s_j\) with the digit \(\hat C_j = 1\) and the other digits 0.
- \(s'_j\) with the digit \(\hat C_j = 2\) and the other digits 0.
The target value \(t_{\phi}\) has
- the digit \(\hat x_i = 1\) for each variable \(x_i\), and
- the digit \(\hat C_j = 4\) for each clause \(C_j\).

Example

Consider the 3-CNF formula \(\phi = C_1 \land C_2 \land C_3 \land C_4\), where

\(C_1 = (x_1 \lor x_2 \lor \neg x_3)\)
\(C_2 = (x_1 \lor \neg x_2 \lor x_3)\)
\(C_3 = (\neg x_1 \lor x_2 \lor x_3)\)
\(C_4 = (\neg x_1 \lor \neg x_2 \lor \neg x_3)\)

Observe that an assignment satisfies the formula iff it assigns an even number of \(x_1\), \(x_2\) and \(x_3\) to true. The corresponding \(\SUBSETSUM\) instance \(\Tuple{S_{\phi}, t_{\phi}}\), where \(S_{\phi} = \{1001100,1000011,101010,100101,10110,11001,1000,2000,100,200,10,20,1,2\}\) and \(t_{\phi} = 1114444\), is shown below.

The subset \(S'\) of \(S_{\phi}\) highlighted with green in the figure is a solution to \(\Tuple{S_{\phi}, t_{\phi}}\). The assignment \(\TA = \{x_1 \mapsto \False,x_2 \mapsto \True,x_3\mapsto\True\}\) corresponding to \(S'\) satisfies the formula \(\phi\).

The correctness of the reduction can be argumented as follows:

Suppose that an assignment \(\TA\) satisfies \(\phi\). We can build a corresponding \(S' \subseteq S_{\phi}\) summing to \(t_{\phi}\) as follows.
- First, for each variable \(x_i\): If \(\TA(x_i) = \True\) for a variable \(x_i\), then include \(v_i\) in \(S'\). Otherwise, include \(v'_i\) in \(S'\).
- At this point, the digit \(\hat C_j\) in the sum is 1, 2, or 3.
- For each clause \(C_j\), include the slack variable \(s_j\), \(s'_j\) or both so that the digit \(\hat C_j\) in the sum becomes \(4\).
In the other direction, suppose that a set \(S' \subseteq S_{\phi}\) sums to \(t_{\phi}\). We build a truth assignment \(\TA\) that satisfies \(\phi\) as follows.
- First note that \(S'\) contains either \(v_i\) or \(v'_i\) (but not both) for each variable \(x_i\) as the digit \(\hat x_i = 1\) in \(t_{\phi}\).
- If \(v_i \in S'\), let \(\TA(x_i) = \True\), otherwise let \(\TA(x_i) = \False\).
- Now at least one literal in each clause \(C_j\) is true under \(\TA\) because the slack variables \(s_j\) alone can only sum the digit \(\hat C_j\) up to 3 but 4 is required in \(t_{\phi}\).