\(\newcommand{\Java}{\href{http://java.com/en/}{Java}}\)
\(\newcommand{\Python}{\href{https://www.python.org/}{Python}}\)
\(\newcommand{\CPP}{\href{http://www.cplusplus.com/}{C++}}\)
\(\newcommand{\ST}[1]{{\Blue{\textsf{#1}}}}\)
\(\newcommand{\PseudoCode}[1]{{\color{blue}\textsf{#1}}}\)
\(%\newcommand{\subheading}[1]{\textbf{\large\color{aaltodgreen}#1}}\)
\(\newcommand{\subheading}[1]{\large{\usebeamercolor[fg]{frametitle} #1}}\)
\(\newcommand{\Blue}[1]{{\color{flagblue}#1}}\)
\(\newcommand{\Red}[1]{{\color{aaltored}#1}}\)
\(\newcommand{\Emph}[1]{\emph{\color{flagblue}#1}}\)
\(\newcommand{\Engl}[1]{({\em engl.}\ #1)}\)
\(\newcommand{\Pointer}{\raisebox{-1ex}{\huge\ding{43}}\ }\)
\(\newcommand{\Set}[1]{\{#1\}}\)
\(\newcommand{\Setdef}[2]{\{{#1}\mid{#2}\}}\)
\(\newcommand{\PSet}[1]{\mathcal{P}(#1)}\)
\(\newcommand{\Card}[1]{{\vert{#1}\vert}}\)
\(\newcommand{\Tuple}[1]{(#1)}\)
\(\newcommand{\Implies}{\Rightarrow}\)
\(\newcommand{\Reals}{\mathbb{R}}\)
\(\newcommand{\Seq}[1]{(#1)}\)
\(\newcommand{\Arr}[1]{[#1]}\)
\(\newcommand{\Floor}[1]{{\lfloor{#1}\rfloor}}\)
\(\newcommand{\Ceil}[1]{{\lceil{#1}\rceil}}\)
\(\newcommand{\Path}[1]{(#1)}\)
\(%\newcommand{\Lg}{\lg}\)
\(\newcommand{\Lg}{\log_2}\)
\(\newcommand{\BigOh}{O}\)
\(\newcommand{\Oh}[1]{\BigOh(#1)}\)
\(\newcommand{\todo}[1]{\Red{\textbf{TO DO: #1}}}\)
\(\newcommand{\NULL}{\textsf{null}}\)
\(\newcommand{\Insert}{\ensuremath{\textsc{insert}}}\)
\(\newcommand{\Search}{\ensuremath{\textsc{search}}}\)
\(\newcommand{\Delete}{\ensuremath{\textsc{delete}}}\)
\(\newcommand{\Remove}{\ensuremath{\textsc{remove}}}\)
\(\newcommand{\Parent}[1]{\mathop{parent}(#1)}\)
\(\newcommand{\ALengthOf}[1]{{#1}.\textit{length}}\)
\(\newcommand{\TRootOf}[1]{{#1}.\textit{root}}\)
\(\newcommand{\TLChildOf}[1]{{#1}.\textit{leftChild}}\)
\(\newcommand{\TRChildOf}[1]{{#1}.\textit{rightChild}}\)
\(\newcommand{\TNode}{x}\)
\(\newcommand{\TNodeI}{y}\)
\(\newcommand{\TKeyOf}[1]{{#1}.\textit{key}}\)
\(\newcommand{\PEnqueue}[2]{{#1}.\textsf{enqueue}(#2)}\)
\(\newcommand{\PDequeue}[1]{{#1}.\textsf{dequeue}()}\)
\(\newcommand{\Def}{\mathrel{:=}}\)
\(\newcommand{\Eq}{\mathrel{=}}\)
\(\newcommand{\Asgn}{\mathrel{\leftarrow}}\)
\(%\newcommand{\Asgn}{\mathrel{:=}}\)
\(%\)
\(% Heaps\)
\(%\)
\(\newcommand{\Downheap}{\textsc{downheap}}\)
\(\newcommand{\Upheap}{\textsc{upheap}}\)
\(\newcommand{\Makeheap}{\textsc{makeheap}}\)
\(%\)
\(% Dynamic sets\)
\(%\)
\(\newcommand{\SInsert}[1]{\textsc{insert}(#1)}\)
\(\newcommand{\SSearch}[1]{\textsc{search}(#1)}\)
\(\newcommand{\SDelete}[1]{\textsc{delete}(#1)}\)
\(\newcommand{\SMin}{\textsc{min}()}\)
\(\newcommand{\SMax}{\textsc{max}()}\)
\(\newcommand{\SPredecessor}[1]{\textsc{predecessor}(#1)}\)
\(\newcommand{\SSuccessor}[1]{\textsc{successor}(#1)}\)
\(%\)
\(% Union-find\)
\(%\)
\(\newcommand{\UFMS}[1]{\textsc{make-set}(#1)}\)
\(\newcommand{\UFFS}[1]{\textsc{find-set}(#1)}\)
\(\newcommand{\UFCompress}[1]{\textsc{find-and-compress}(#1)}\)
\(\newcommand{\UFUnion}[2]{\textsc{union}(#1,#2)}\)
\(%\)
\(% Graphs\)
\(%\)
\(\newcommand{\Verts}{V}\)
\(\newcommand{\Vtx}{v}\)
\(\newcommand{\VtxA}{v_1}\)
\(\newcommand{\VtxB}{v_2}\)
\(\newcommand{\VertsA}{V_\textup{A}}\)
\(\newcommand{\VertsB}{V_\textup{B}}\)
\(\newcommand{\Edges}{E}\)
\(\newcommand{\Edge}{e}\)
\(\newcommand{\NofV}{\Card{V}}\)
\(\newcommand{\NofE}{\Card{E}}\)
\(\newcommand{\Graph}{G}\)
\(\newcommand{\SCC}{C}\)
\(\newcommand{\GraphSCC}{G^\text{SCC}}\)
\(\newcommand{\VertsSCC}{V^\text{SCC}}\)
\(\newcommand{\EdgesSCC}{E^\text{SCC}}\)
\(\newcommand{\GraphT}{G^\text{T}}\)
\(%\newcommand{\VertsT}{V^\textup{T}}\)
\(\newcommand{\EdgesT}{E^\text{T}}\)
\(%\)
\(% NP-completeness etc\)
\(%\)
\(\newcommand{\Poly}{\textbf{P}}\)
\(\newcommand{\NP}{\textbf{NP}}\)
\(\newcommand{\PSPACE}{\textbf{PSPACE}}\)
\(\newcommand{\EXPTIME}{\textbf{EXPTIME}}\)
Topological sort
A topological sort, or topological ordering,
for a directed acyclic graph \(\Tuple{\Verts,\Edges}\)
is a linear ordering of its vertices \(\Verts\) such that
for each edge \(\Tuple{u,v} \in \Edges\),
it holds that \(u\) appears before \(v\) in the ordering.
Naturally, directed graphs with cycles do not
have such linear orderings and cannot be topologically sorted.
Example
Consider again the toy example DAG from our previous example, shown below.
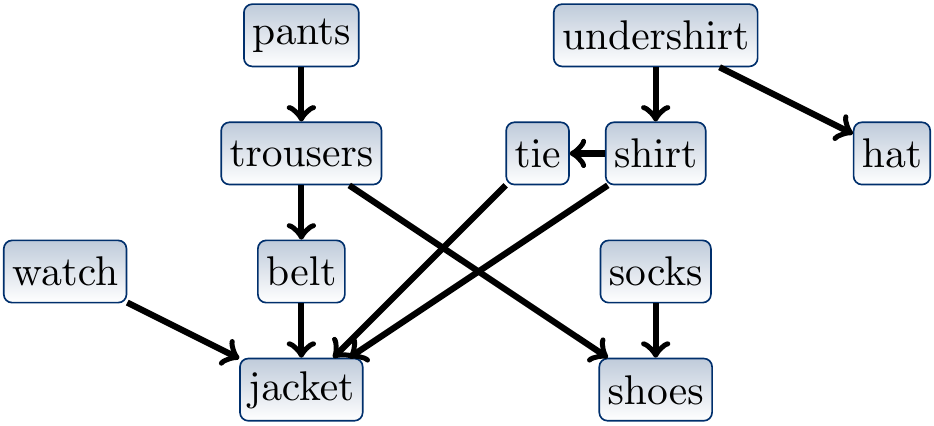
Two possible topological sorts for the DAG are:
pants,undershirt,trousers,shirt,belt,tie,socks,shoes,watch,jacket,hat
watch,pants,socks,trousers,shoes,belt,undershirt,hat,shirt,tie,jacket
A topological sort can be obtained easily with Depth-first search:
Perform depth-first search on the graph,
but when a vertex is finished (colored black),
add it in the front of a linked list, and
at the end, return the list.
The key idea for the correctness of this algorithm is
the following fact:
During a depth-first search in a DAG, when a vertex is colored black, all the vertices reachable from it are black.
In DAGs such reachable vertices cannot be gray because that would mean that the graph has a cycle.
Thus in the topological sorting algorithm given above,
all the successors of the vertex that is being colored black are already black and later in the produced list giving the ordering.
Topological sorting can be done in time \(\Oh{\Card{V}+\Card{E}}\) as
the algorithm above is a simple variant of depth-first search.
Other algorithms also exists, see this Wikipedia page.
Example
Consider again the DAG shown below.
The time-stamps produced by an arbitrary depth-first search on it are
also shown.
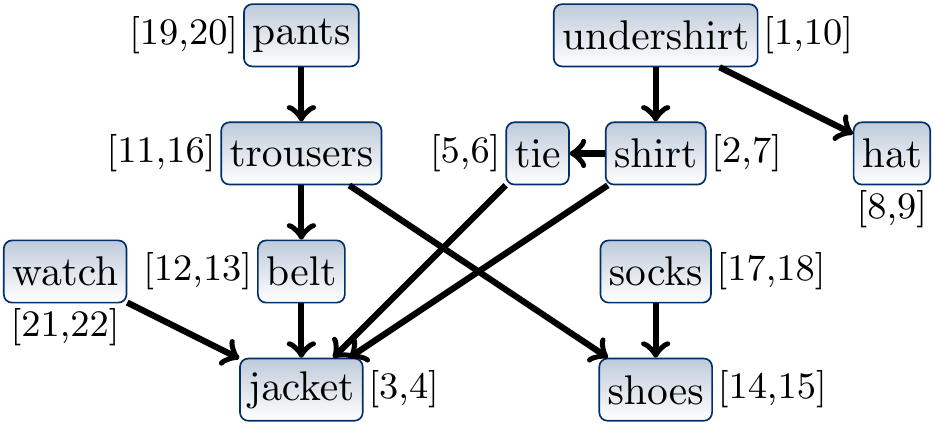
The topological sort produced by this particular depth-first search is
watch,pants,socks,trousers,shoes,belt,undershirt,hat,shirt,tie,jacket

