Extra: B-trees

This section is not included in the examination requirements of the course.

The red-black trees are equivalent to 2-3-4 trees, which in turn are a subclass of B-trees. B-trees are a self-balancing tree data structure in which inserting, searching, minimum, successor etc. can be done in logarithmic time. Unlike binary search trees, B-tree nodes can have more than two children. The amount of data in a node can be selected to match the block size of the applied hard drive / file system (usually some kilobytes). Therefore, B-trees are used for indexing in applications where the data is stored outside the main memory. In particular, they are used to maintain indexes in data base systems (such as MongoDB, just to name one). One can try this external visualization tool for inspecting how B-trees work.

In B-trees of order \(m\):

• ​ Each node has at most \(m\) children

• ​ Each internal non-root node has at least \(\lceil m/2 \rceil\) children

• ​ All the leafs are at the same level

• ​ An internal node has \(m-1\) keys

• ​ The keys “in the left” of an internal-node key \(k\) are at most \(k\)

• ​ The keys “in the right” of an internal-node key \(k\) are at least \(k\)

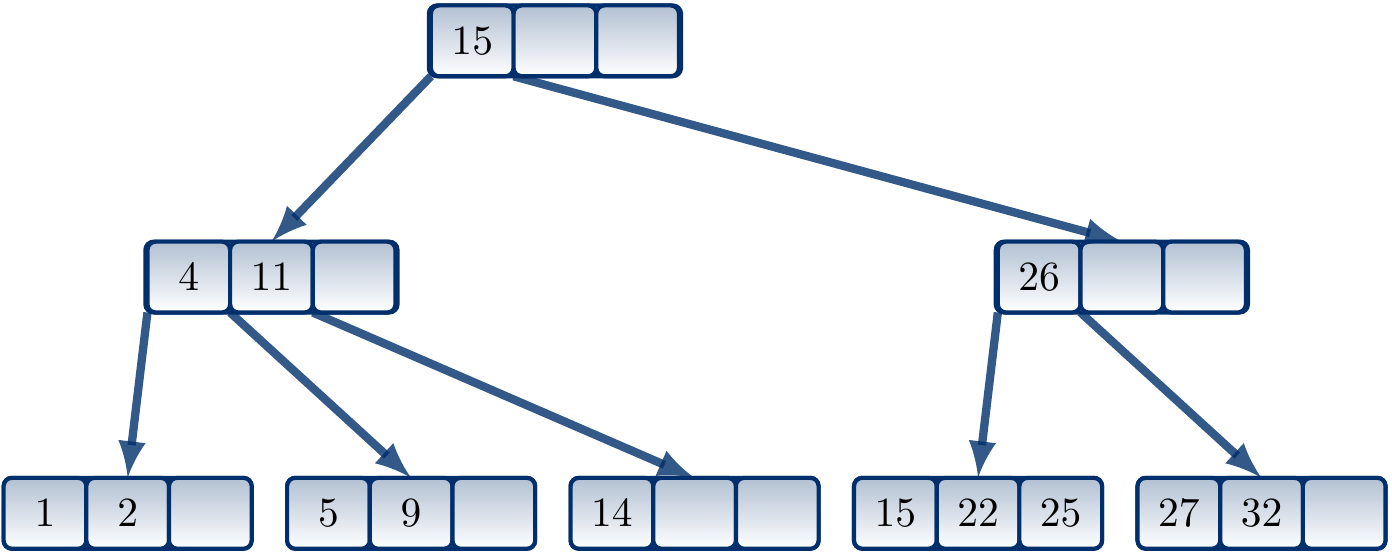
Example

Consider the following B-tree of order \(4\).

Suppose that we insert an element having the key 14 in the tree.

• ​ The element should be inserted in the leaf with the keys \(5\), \(9\) and \(11\) but it is full.

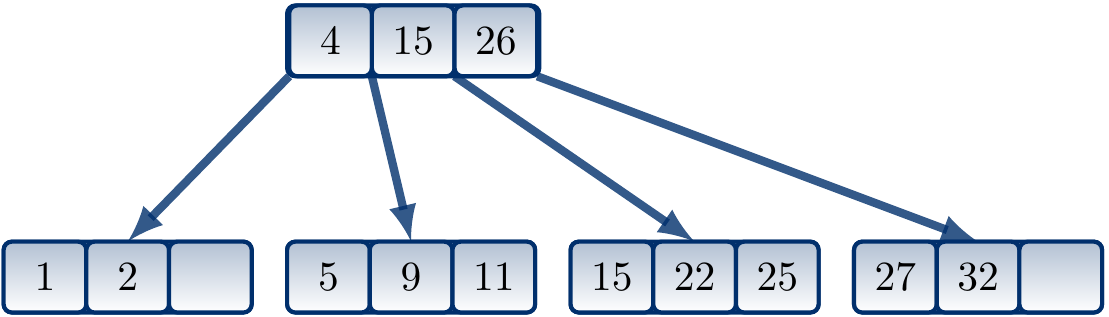
• ​ The leaf node is split in two and \(14\) is inserted in the latter. The “median” key \(11\) is inserted to the parent node of the leaf.

• ​ But the parent node is full as well so it must also be split.

• ​ As it was the root, the depth of the tree increases by one.

The resulting B-tree is shown below.