$$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$

$$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$ $$

Greedy Algorithms

In the two last examples of dynamic programming, we had to consider many sub-problems to solve a problem. For instance, in the rodding cutting problem we had to consider all the possible ways of making the first cut. Similarly, in the LCS problem there were two potential ways for obtaining the optimal solution when the last symbols in the sequence were not the same.

However, sometimes it is possible to greedily select just one case and thus reduce the problem into one smaller sub-problem. We next consider one such simple greedy algorithm. In the graphs rounds, we’ll see other greedy algorithms when we study the minimum spanning tree algorithms.

Example IV: Activity-selection problem

Assume that we are given a finite set of activities $A=\{a_1,...,a_n\}$. Each activity $a_i$ is associated with

• ​ a start time $s_i$, and

• ​ a finish time $f_i$ with $s_i<f_i$.

An activity executes in the half-open interval $[s_i,f_i)$. Two activities, $a_i$ and $a_j$ for $i\ne j$, are said to be compatible if they do not execute at the same time, meaning that either $f_i\le s_j$ or $f_j\le s_i$. Our task is find a maximal compatible subset of $A$, i.e., a subset $A^{\prime }\subseteq A$ of largest size such that all the activities in the set are mutually compatible.

Example

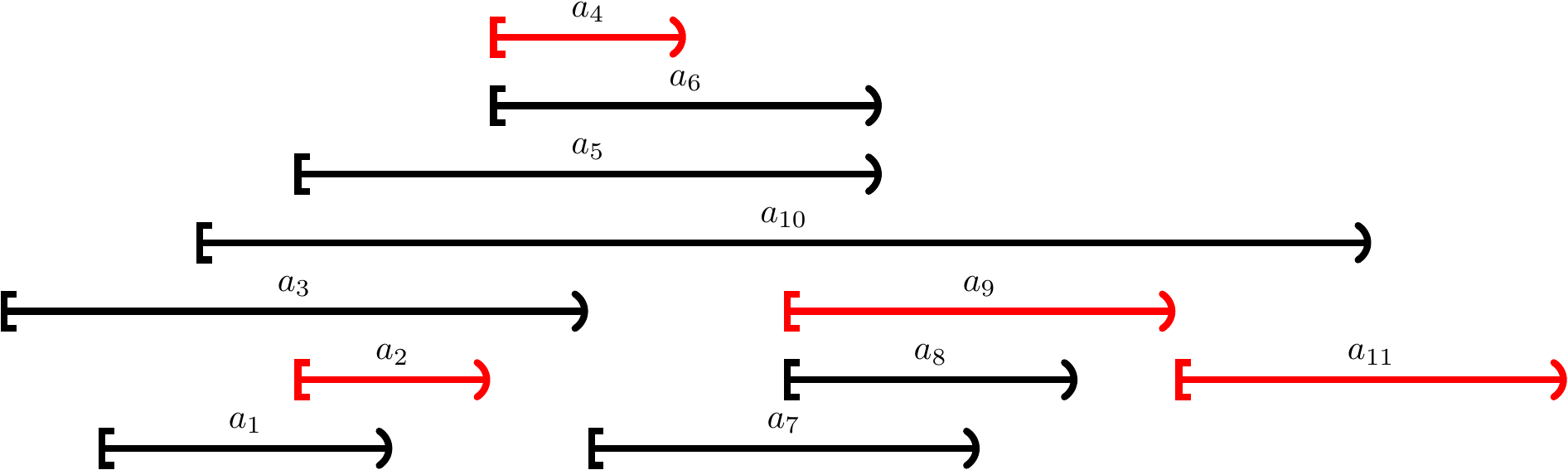
Consider the set of activities $A=\{a_1,...,a_{11}\}$ with

$$\begin{array}{cccccccccccc}i& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11\\ s_i& 1& 3& 0& 5& 3& 5& 6& 8& 8& 2& 12\\ f_i& 4& 5& 6& 7& 9& 9& 10& 11& 12& 14& 16\end{array}$$

A maximal compatible subset is $\{a_2,a_4,a_9,a_{11}\}$.

A dynamic programming formulation

In order to relate dynamic programming and greedy algorithms, let us first see a dynamic programming approach for solving the activity selection problem.

Assume that the set of activities is $A=\{a_1,...,a_n\}$. For obtaining the recursive definition for optimal solutions, let

$$A_{l,u}=\{a_i\in A\mid l\le s_i\wedge f_i\le u\}$$

be the set of activities that start at $l$ or later and finish at latest at $u$. If we use $L=\underset{i\in [1..n]}{min}{s}_i$ and $U=\underset{i\in [1..n]}{max}{f}_i$, then the original problem instance $A$ is $A_{L,U}$.

Each (sub-)problem on $A_{l,u}$ has the optimal sub-solution property:

• ​ Take any activity $a_i\in A_{l,u}$

• ​ Let $A_{l,s_i}^{\prime }$ and $A_{f_i,u}^{\prime }$ be any maximal compatible subsets for the sets $A_{l,s_i}$ of activities in $A_{l,u}$ ending before $a_i$ and $A_{f_i,u}$ of activities in $A_{l,u}$ starting after $a_i$.

• ​ Then $A_{l,u\text{ at }i}^{\prime }=A_{l,s_i}^{\prime }\cup \{a_i\}\cup A_{f_i,u}^{\prime }$ is a maximal compatible subset for $A_{l,u}$ that contains $a_i$.

Thus a maximal compatible subset for $A_{l,u}$ is

$$A_{l,u}^{\prime }=\underset{a_j\in A_{l,u}}{max}{A}_{l,u\text{ at }j}^{\prime }.$$

The solution for the original problem is $A_{L,U}^{\prime }$. We now have a recursive definition that can be turned into a dynamic programming algorithm. Note that the number of sub-problems $A_{l,u}$ one has to consider is at most $(n+1)\times (n+1)$ because (i) the start index $l$ of each $A_{l,u}$ is either $L$ or an ending time of an activity, and (ii) the ending index $u$ of each $A_{l,u}$ is either $U$ or a starting time of an activity. Thus the dynamic programming approach can be made to work in polynomial time. On the contrary, the straighforward approach of

• ​ enumerating all the subsets of $A$,

• ​ checking the compatibility of each, and

• ​ remembering a largest compatible one

would require at least exponential time as there are exponetially many subsets.

In Scala, we can implement the dynamic programming algorithm as follows. Note that the implementation is not very well optimized.

def activitySelectorDynprog(acts: Set[(Int,Int)]) =
  require(acts.forall(a => a._1 >= 0 && a._1 < a._2))
  val mem = collection.mutable.Map[Set[(Int,Int)],Set[(Int,Int)]]()
  def inner(current: Set[(Int,Int)]): Set[(Int,Int)] =
    mem.getOrElseUpdate(current, {
      var best = Set[(Int,Int)]()
      for act <- current do
        val earlier = current.filter(a => a._2 <= act._1)
        val later = current.filter(a => act._2 <= a._1)
        val earlierResult = inner(earlier)
        val laterResult = inner(later)
        if earlierResult.size + 1 + laterResult.size > best.size then
          best = (earlierResult ++ laterResult) + act
      best
    })
  inner(acts)

Running our example with it, we get:

scala> val acts = Set((1,4),(3,5),(0,6),(5,7),(3,9),(5,9),(6,10),
                      (8,11),(8,12),(2,14),(12,16))
acts: Set[(Int, Int)] = HashSet((8,12), (1,4), (8,11), (5,9), (3,9), (3,5), (12,16), (0,6), (5,7), (6,10), (2,14))

scala> activitySelectorDynprog(acts).toVector.sortBy(_._1)
res1: Vector[(Int, Int)] = Vector((1,4), (5,7), (8,12), (12,16))

The greedy approach

The activity selection problem has a property that we can use to obtain an even faster and simpler algorithm. Namely, we do not have to consider all the activities in a subset but can

• ​ just select one that finishes as early as possible, and

• ​ then, consider the sub-problem obtained by removing that activity and all the activities that are not compatible with it.

This optimization is based on the observation that if we have a maximal compatible subset that does not contain an activity $a_i$ that finishes as early as possible, we can substitute one that is in the set with $a_i$ and obtain a compatible subset of the same maximal size. This is formalized in the following theorem.

Theorem

Let $A^{\prime }\subseteq A$ be a maximal subset of compatible activities, $a_i$ an activity with the earliest finish time among those in $A$, and $a_j$ be the activity with the earliest finish time among those in $A^{\prime }$. Then $(A^{\prime }\setminus \{a_j\})\cup \{a_i\}$ is also a maximal subset of compatible activities.

Proof

If $i=j$, we are done.

Otherwise, it must be that $f_i\le f_j$. As $a_j$ is the activity with the earliest finish time among those in $A^{\prime }$, $A^{\prime }$ does not contain any $a_k$, $k\ne j$, with $s_k\le f_i$. Therefore, it is safe to substitute $a_j$ with $a_i$ in $A^{\prime }$ and obtain a set of compatible activities that has the same maximal size.

Example

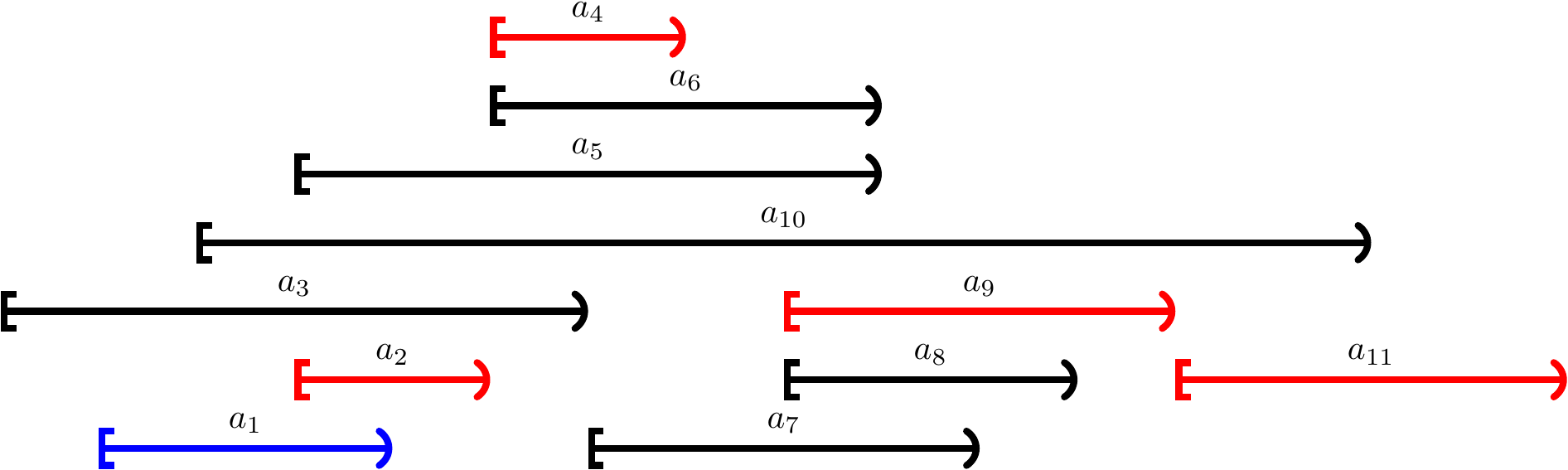
Consider again the activities $A=\{a_1,...,a_{11}\}$, where

$$\begin{array}{cccccccccccc}i& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11\\ s_i& 1& 3& 0& 5& 3& 5& 6& 8& 8& 2& 12\\ f_i& 4& 5& 6& 7& 9& 9& 10& 11& 12& 14& 16\end{array}$$

One maximal compatible subset is $\{a_2,a_4,a_9,a_{11}\}$. It does not contain the activity $a_1$ with the earliest finish time among those in $A$. If we substitute the activity $a_2$ having the earliest finish time among those in $A$ with the activity $a_1$, the result is the maximal compatible subset $\{a_1,a_4,a_9,a_{11}\}$.

Observe that $\{a_4,a_9,a_{11}\}$ is a maximal compatible subset of the “reduced” sub-problem $\{a_4,a_6,a_7,a_8,a_9,a_{11}\}$ obtained by removing $a_1$ and all the activities that are not compatible with it.

In Scala, we can implement the greedy algorithm as follows:

def activitySelectorGreedy(acts: Set[(Int,Int)]) =
  require(acts.forall(a => a._1 >= 0 && a._1 < a._2))
  val sorted = acts.toVector.sortBy(_._2)
  val sol = collection.mutable.ArrayBuffer[(Int,Int)]()
  var time = Int.MinValue
  for act <- sorted do
    if act._1 >= time then
      sol += act
      time = act._2
  sol.toSet

Running our example with it, we get:

scala> val acts = Set((1,4),(3,5),(0,6),(5,7),(3,9),(5,9),(6,10),(8,11),(8,12),(2,14),(12,16))
acts: Set[(Int, Int)] = HashSet((8,12), (1,4), (8,11), (5,9), (3,9), (3,5), (12,16), (0,6), (5,7), (6,10), (2,14))
                                                                                
scala> activitySelectorGreedy(acts).toVector.sortBy(_._1)
res0: Vector[(Int, Int)] = Vector((1,4), (5,7), (8,11), (12,16))