Traversing trees¶

In many situations it is required to traverse all the nodes in a rooted tree. This can be done in many ways, depending in which order the nodes are visited:

preorder traversal first visits the current node and then (recursively) its children one-by-one.
inorder traversal, especially on binary trees, first (recursively) visits the left child, then the node itself and then (recursively) the right child.
postorder traversal first visits (recursively) all the children one-by-one and then the node itself.
level order traversal, which is not so common, visits the nodes level-by-level left-to-right starting from the root node.

In pseudo-code, we can express each of the traversal methods as follows. Observe the use of queues in the level order traversal.

traverse-preorder(tree \( T \)):
  def traverse(\( n \)):
    visit(\( n \))
    for each child \( c \) of \( n \):
      traverse(\( c \))
  traverse(\( \TRootOf{T} \))
 

traverse-inorder(tree \( T \)):
  def traverse(\( n \)):
    traverse(\( \TLChildOf{n} \))
    visit(\( n \))
    traverse(\( \TRChildOf{n} \))
  traverse(\( \TRootOf{T} \))
 

traverse-postorder(tree \( T \)):
  def traverse(\( n \)):
    for each child \( c \) of \( n \):
      traverse(\( c \))
    visit(\( n \))
  traverse(\( \TRootOf{T} \))
 

traverse-levelorder(tree \( T \)):
  \( level \Asgn  \)new Queue
  \( \PEnqueue{level}{\TRootOf{T}} \)
  while \( level \) is non-empty:
    \( nextLevel \Asgn  \)new Queue
    while \( level \) is non-empty:
      \( n \Asgn \PDequeue{level} \)
      visit(\( n \))
      for each child \( c \) of \( n \):
        \( \PEnqueue{nextLevel}{c} \)
    \( level \Asgn nextLevel \)
 

Example

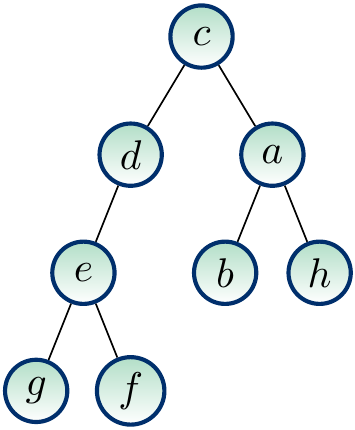
The visiting orders for the nodes in the tree shown below are as follows.

Preorder: \(c,d,e,g,f,a,b,h\)
Inorder: \(g,e,f,d,c,b,a,h\)
Postorder: \(g,f,e,d,b,h,a,c\)
Level order: \(c,d,a,e,b,h,g,f\)

In practise, tree traversal functions may mix orders.

Example

The following Scala code shows how to print arithmetic expressions in the prefix, infix, and postfix notations.

abstract class Expr {
  def prefixStr: String
  def infixStr: String
  def postfixStr: String
}
case class Negate(expr: Expr) extends Expr {
  def prefixStr: String = "Negate("+expr.prefixStr+")"
  def infixStr: String = "-"+expr.infixStr
  def postfixStr: String = expr.postfixStr + " -"
}
case class Add(left: Expr, right: Expr) extends Expr {
  def prefixStr: String = "Add("+left.prefixStr+","+right.prefixStr+")"
  def infixStr: String = "("+left.infixStr+"+"+right.infixStr+")"
  def postfixStr: String = left.postfixStr+" "+right.postfixStr+" +"
}
case class Multiply(left: Expr, right: Expr) extends Expr {
  def prefixStr: String = "Multiply("+left.prefixStr+","+right.prefixStr+")"
  def infixStr: String = "("+left.infixStr+"*"+right.infixStr+")"
  def postfixStr: String = left.postfixStr + " "+ right.postfixStr + " *"
}
case class Var(name: String) extends Expr {
  def prefixStr: String = "Var(\""+name+"\")"
  def infixStr: String = name
  def postfixStr: String = name
}
case class Num(value: Double) extends Expr {
  def prefixStr: String = "Num("+value.toString+")"
  def infixStr: String = value.toString
  def postfixStr: String = value.toString
}

val e = Negate(Add(Multiply(Num(2.0),Var("x")),Var("y")))
println(e.prefixStr)
println(e.infixStr)
println(e.postfixStr)

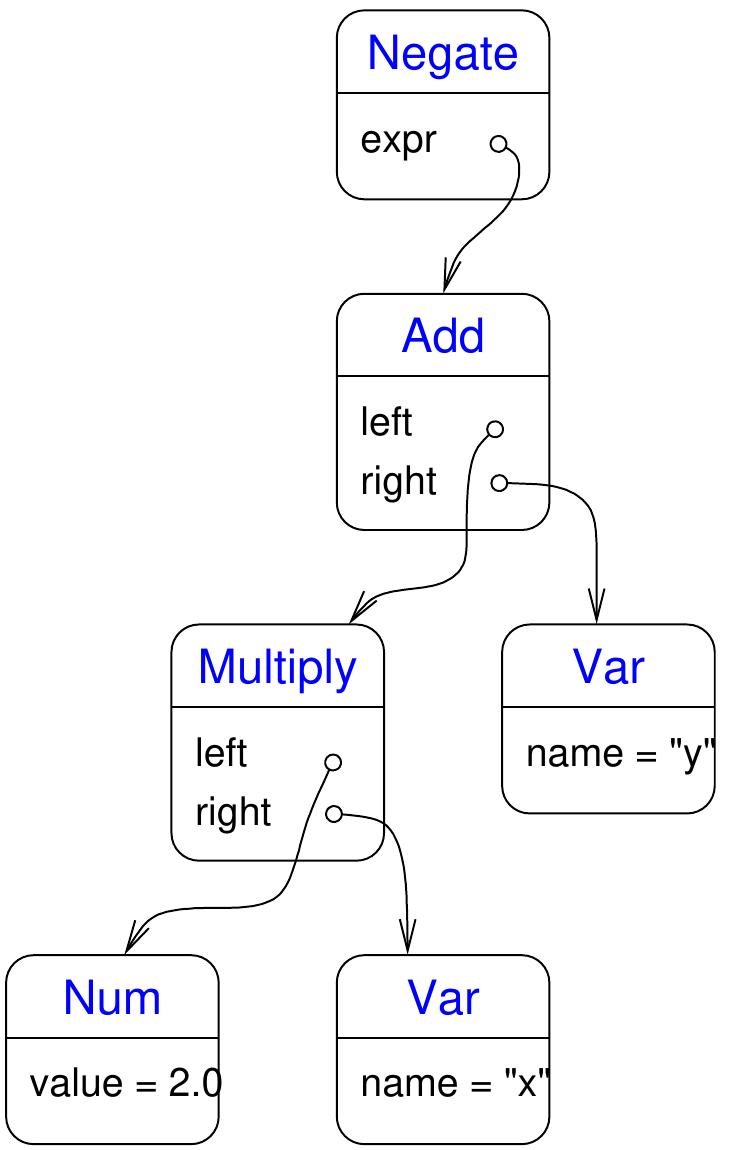
The parse tree corresponding to the expression \(-(2.0x + y)\) is obtained with val e = Negate(Add(Multiply(Num(2.0),Var(“x”)),Var(“y”))) is shown below.

e.prefixStr produces Negate(Add(Multiply(Num(2.0),Var(“x”)),Var(“y”))).
e.infixStr produces -((2.0*x)+y).
e.postfixStr gives 2.0 x * y + -.

The postfix notation does not need parentheses and it is easy to read and evaluate from the textual representation by using a stack (see e.g. this article).