Problems in NP (Non-deterministic Polynomial time)¶
There are two (and even more) equivalent ways to characterize the decision problems in the class \(\NP\):
Problems that can be solved in polynomial time with non-deterministic (Turing) machines.
Such non-deterministic machines can compute the same functions as our current CPUs in polynomial time. In addition, they can “branch” their computations into many “simultaneous” computations and return a solution if at least one of the branches finds a solution. They cannot be implemented with the current hardware but are rather a conceptual tool; more on non-determinism in the CS-C2160 ToC course.
Problems for whose “yes” instances, and only those, have a certificate that is both
reasonably small (i.e., of polynomial size w.r.t. the input), and
easy to verify (i.e., in polynomial time w.r.t. the input).
However, the certificates are not necessarily easy to find (or to prove non-existent)!
In most cases, one can think that a “certificate” is a synonym for a “solution”.
The subset-sum problem¶
As a first example, consider the \(\SUBSETSUM\) problem.
Definition: \(\SUBSETSUM\)
Instance: A set \(S\) of integers and a target value \(t\).
Question: Does \(S\) have a subset \(S' \subseteq S\) such that \(\sum_{s \in S'}s = t\)?
For each instance \(\Tuple{S,t}\) with the “yes” answer (and for only those), a certificate is a set \(S'\) of integers such that \(S' \subseteq S\) and \(\sum_{v \in S'} = t\). The set \(S'\) is obviously of polynomial size w.r.t. the instance \(\Tuple{S,t}\) as \(S' \subseteq S\). On can also easily check in polynomial time whether the certificate is valid, i.e., whether it holds that (i) \(S' \subseteq S\) and (ii) \(\sum_{v \in S'} = t\). Thus the \(\SUBSETSUM\) problem is in the class \(\NP\).
Example
A certificate for the instance \(\Tuple{S,t}\) with
\(S = \{2, 7, 14, 49, 98, 343, 686, 2409, 2793, 16808, 17206, 117705, 117993\}\) and
\(t = 138457\)
is \(S' = \Set{2, 7, 98, 343, 686, 2409, 17206, 117705}\).
The instance \(\Tuple{S,t}\) with
\(S = \{2, 7, 14, 49\}\) and
\(t = 15\)
does not have any certificates and the answer for it is “no”.
Propositional satisfiability¶
Propositional formulas are built on
Boolean variables, and
connectives of unary negation \(\neg\), binary disjunction \(\lor\) and binary conjunction \(\land\).
In Scala terms, the negation \(\neg\) corresponds to
the unary operation !,
the conjunction \(\land\) to the binary operation &&,
and
the disjunction \(\lor\) to ||.
The difference is that in Scala, a Boolean variable always has a value
(either true of false).
Therefore, in Scala a Boolean expression (a && !b) || (!a && b)
can be evaluated at any time point to some value.
In the propositional formula level, a variable is like an unknown variable
in mathematics: it does not have a value unless we associate one by some
mapping etc.
Thus the propositional formula \((a \land \neg b) \lor (\neg a \land b)\)
cannot be evaluated unless we give values to \(a\) and \(b\):
an assignment \(\TA\) for a formula \(\phi\) is a mapping
from the variables \(\VarsOf{\phi}\) in the formula to \(\Booleans = \Set{\False,\True}\).
It satisfies the formula if it evaluates the formula to true.
A formula is satisfiable if there is an assignment that satisfies it; otherwise it is unsatisfiable.
Example
The formula
is satisfiable as the assignment \(\TA = \{a \mapsto \True,b \mapsto \False,c \mapsto \True\}\), among 2 others, evaluates it to true.
The formula \((a) \land (\neg a \lor b) \land (\neg b \lor c) \land (\neg c \lor \neg a)\) is unsatisfiable.
Definition: \(\Prob{propositional satisfiability}\), \(\SAT\)
Instance: a propositional formula \(\phi\).
Question: is the formula \(\phi\) satisfiable?
The propositional satisfiability problem can be understood as the problem of deciding whether an equation \(\phi = \True\) has a solution, i.e. deciding whether the variables in \(\phi\) have some values so that the formula evaluates to true. The problem is in \(\NP\) as we can use a satisfying assignment as the certificate:
its size is linear in the number of variables in the formula, and
evaluating the formula to check whether the result is \(\True\) is easy.
To simplify theory and practice, one often uses certain normal forms of formulas:
A literal is a variable \(x_i\) or its negation \(\neg x_i\)
A clause is a disjunction \((l_1 \lor ... \lor l_k)\) of literals
A formula is in 3-CNF (CNF means conjunctive normal form) if it is a conjunction of clauses and each clause has 3 literals over distinct variables. For instance, \((x_1 \lor \neg x_2 \lor x_4) \land (\neg x_1 \lor \neg x_2 \lor x_3) \land (x_2 \lor \neg x_3 \lor x_4)\) is in 3-CNF.
Definition: \(\SATT\)
Instance: a propositional formula in 3-CNF.
Question: is the formula satisfiable?
Some other problems in NP¶
Definition: \(\Prob{Travelling salesperson}\)
Instance: An edge-weighted undirected graph \(\Graph\) and an integer \(k\).
Question: Does the graph have a simple cycle visiting all the vertices and having weight \(k\) or less?
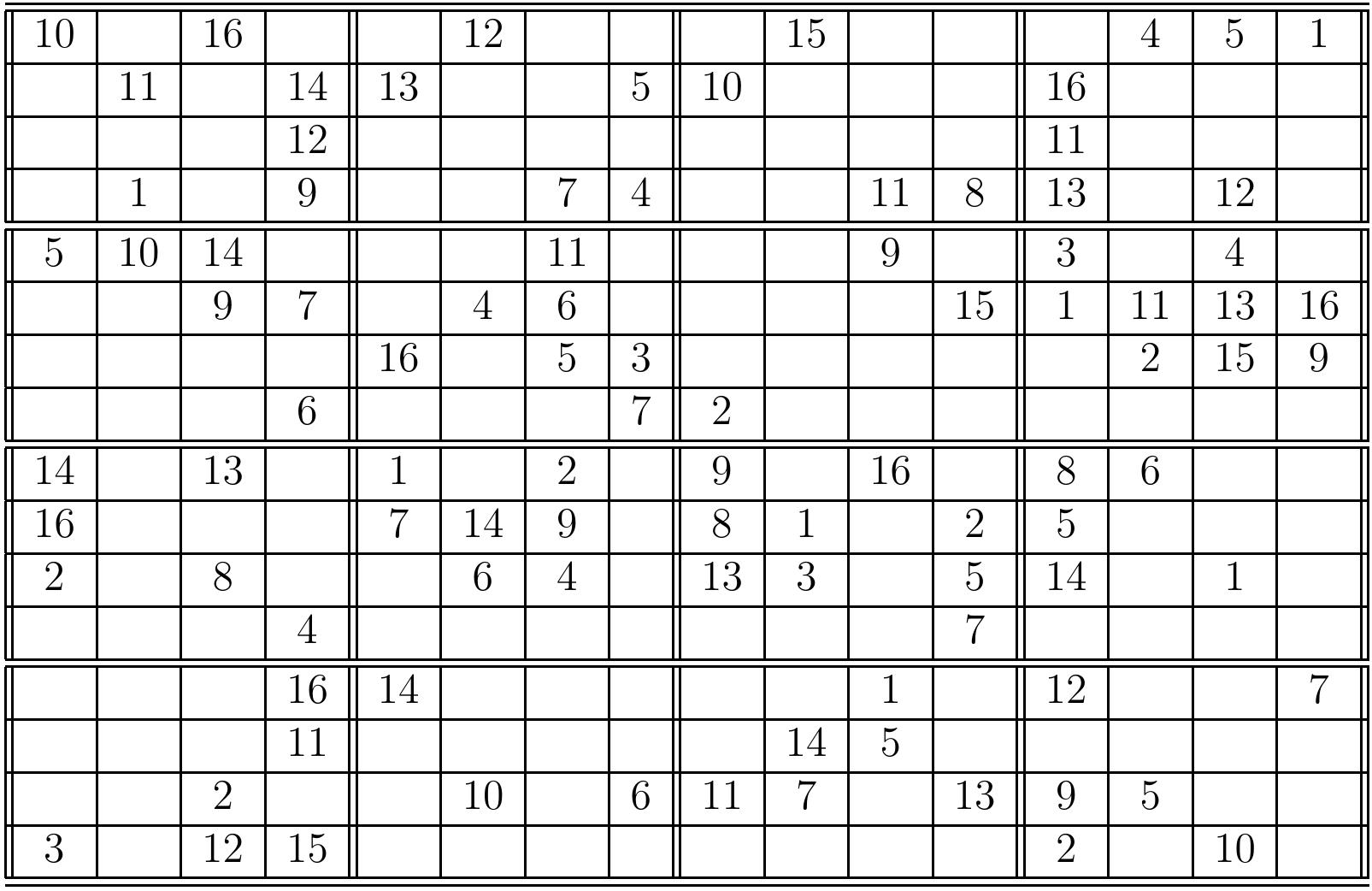
Definition: \(\Prob{Generalized Sudokus}\)
Instance: An \(n \times n\) partially filled Sudoku grid (\(n=k^2\) for some integer \(k \ge 1\)).
Question: Can the Sudoku grid be completed?
Definition: \(\Prob{longest simple path (decision version)}\) problem
Instance: an undirected graph \(\Graph=\Tuple{\Verts,\Edges}\), two vertices \(\Vtx,\Vtx' \in \Verts\), and an integer \(k\).
Question: Is there a simple path of length \(k\) or more from \(\Vtx\) to \(\Vtx'\)?
Definition: \(\MSTDEC\) problem
Instance: A connected edge-weighted and undirected graph \(G=\Tuple{\Verts,\Edges,\UWeights}\) and an integer \(k\).
Question: Does the graph have a spanning tree of weight \(k\) or less?
Definition: \(\Prob{Minimum Steiner tree (decision version)}\) problem
Instance: A connected edge-weighted and undirected graph \(\Graph=\Tuple{\Verts,\Edges,\UWeights}\), a set \(S \subseteq \Verts\), and an integer \(k\).
Question: Does the graph have a tree that spans all the vertices in \(S\) and has weight \(k\) or less?
And hundreds of others…
P versus NP¶
For polynomial-time solvable problems, the instance itself can act as the certificate because we can always compute, in polynomial time, the correct no/yes answer from the instance itself. Therefore, \(\Poly \subseteq \NP\). However, we do not know whether \(\Poly = \NP\). In other words, we do not know whether it is always the case that if a solution is small and easy to check, is it always relatively easy to find it? Most people believe that \(\Poly \neq \NP\) but no-one has yet been able to prove this (or that \(\Poly = \NP\)). We know efficient algorithms for many problems such as \(\Prob{minimum spanning tree}\), \(\Prob{shortest path}\), and so on. But we do not know any efficient algorithms for \(\SUBSETSUM\), \(\SATT\), and hundreds of other (practically relevant) problems in \(\NP\), even though lots of extremely clever people have tried to find ones for decades.