Introduction: sets and maps¶

In this and the next round we are interested in the abstract data types for dynamic sets and maps. Here “dynamic” means that the keys, or (key,value) associations in maps, are inserted, searched for and removed all the time in an online fashion.

Sets¶

A basic API for a set abstract data type could be

insert(k) for inserting the key k in the set,
search(k) for finding whether the key k is in the set, and
remove(k) for deleting the key k from the set.

The figure below shows the set diagrams for two sets of strings, where the latter is obtained by inserting a new string in it.

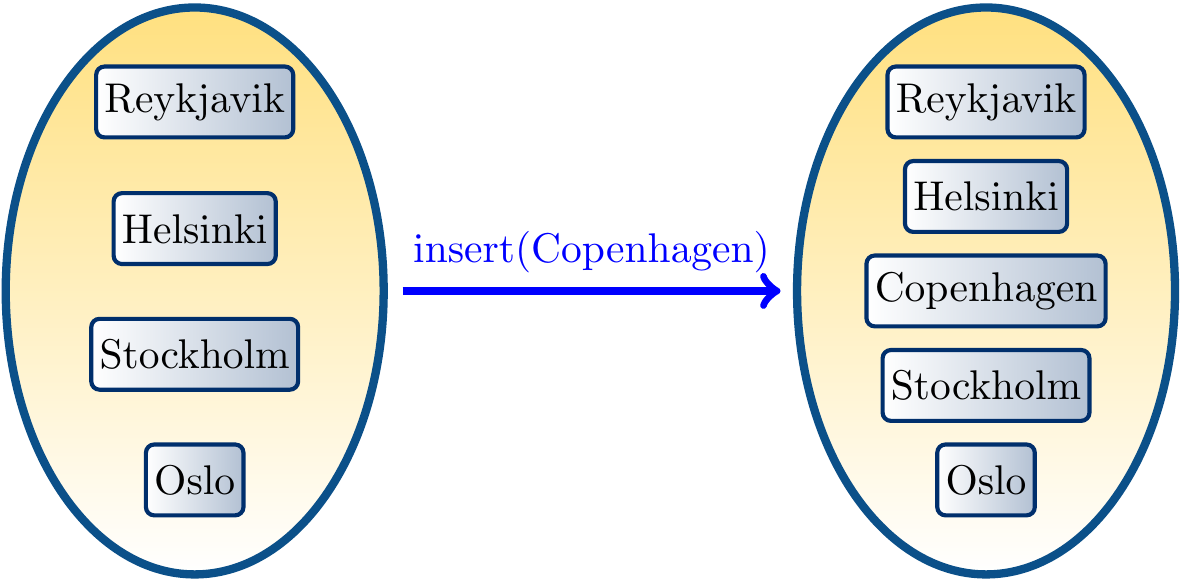
In Scala, this API corresponds to the collection.mutable.Set trait, which is implemented, among others, in the mutable TreeSet and HashSet classes. The methods corresponding to the ones in the asbtract API are

s.add(k) or s += k for inserting key k into the set s,
s.contains(k) or s(k) for checking whether the set s contains the key k, and
s.remove(k) or s -= k for removing the key k from the set s.

In Java, the counterpart is the Set interface. In C++, the standard library contains two classes, set and unordered_set, implementing a variant of the API (the difference is explained below).

Maps¶

For maps, also called dictionaries in some languages, the API also allows associating a value to each key.

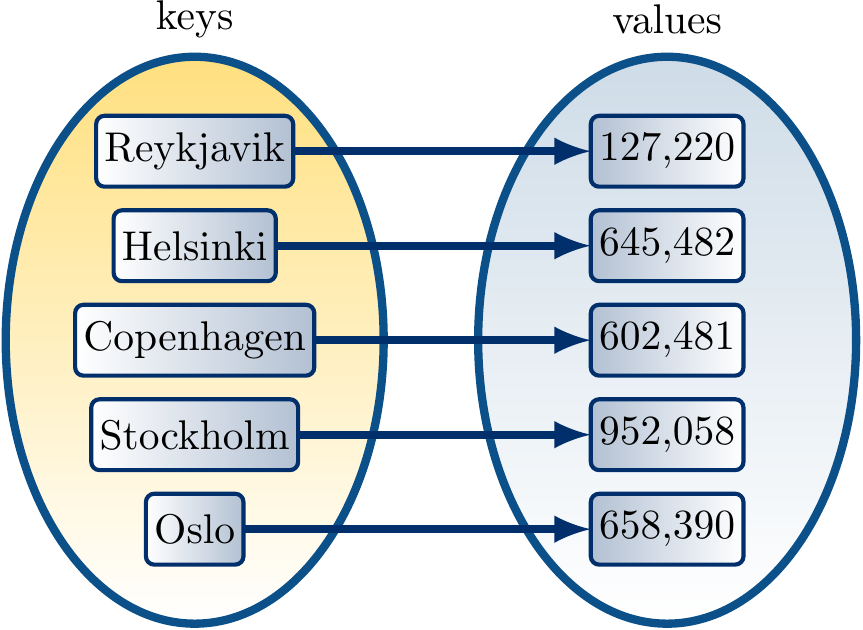
In Scala mutable map trait the methods are called

m.update(k,v) or simply m(k) = v for setting the value of the key k to v in the map m,
m.apply(k) or simply m(k) for getting the value associated with the key k in the map m, and
m.remove(k) for removing the key k from the map m.

In the Java 8 Map interface the methods are called put, get, and remove.

In the C++ standard library map and unordered_map classes, the methods are called

insert, or simply m[k] = v, for a map m, key k, and value v,
m.at(k), or simply m[k], and
m.erase(k).

Ordered sets and maps¶

In this round, we will in fact consider ordered sets and ordered maps that

assume an ordering between the keys, and
allow efficient searching for the smallest, next smallest, etc keys.

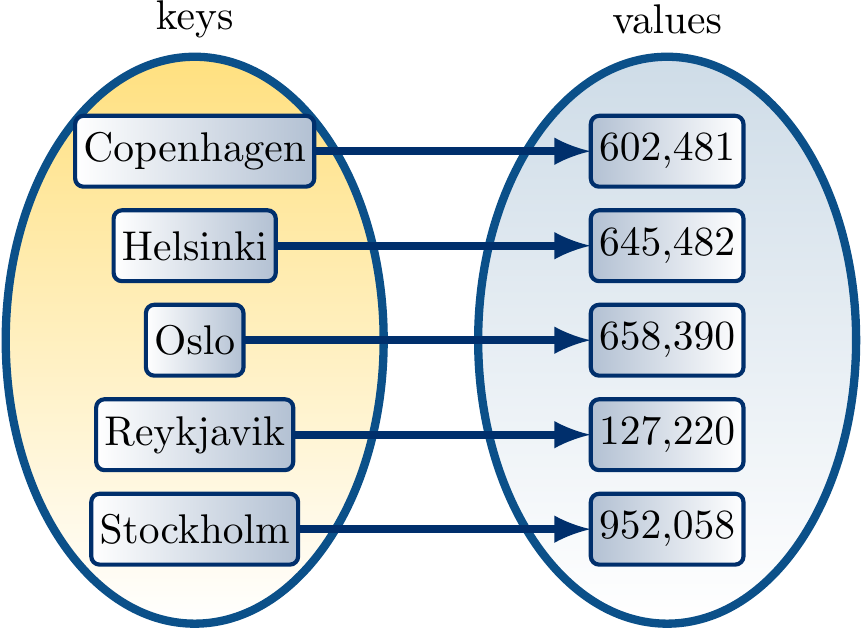
The abstract API of ordered sets extends the basic API with

min for getting the smallest key in the set,
max for getting the largest key in the set,
predecessor(k) for getting the largest key that is smaller than k, and
successor(k) for getting the smallest key that is larger than k.

Our goal is to have data structures and algorithms allowing the operations to be done in logarithmic time in the size of the set. Furthermore, the keys can be listed in ascending order in linear time. Note the difference to the priority queue API of the previous round (Section Priority queues with binary heaps): removing arbitrary keys as well as finding the minimum and successor are now also supported.

In Scala, the TreeSet class implements a variant of the API allowing ordered iteration over the keys in the set.

In the class, firstKey gives the smallest key while lastKey finds the largest key. Note: min and max are slow, linear time generic operations, do not use them.

Note 2: in the current Scala version, val s = collection.mutable.Set() creates a new “hash set” (covered in the next round) in which the operations above take linear time in the worst case. Use val s = collection.mutable.TreeSet() to create an ordered set.
In Java, the TreeSet API is close to the abstract one:
- first gives the smallest key,
- last gives the largest key,
- higher(k) gives the smallest key that is larger than k, and
- lower(k) gives the largest key that is smaller than k.
The C++ standard library has the set class.
For maps, the corresponding classes are TreeMap in Scala, TreeMap in Java, and map in the C++ standard library.